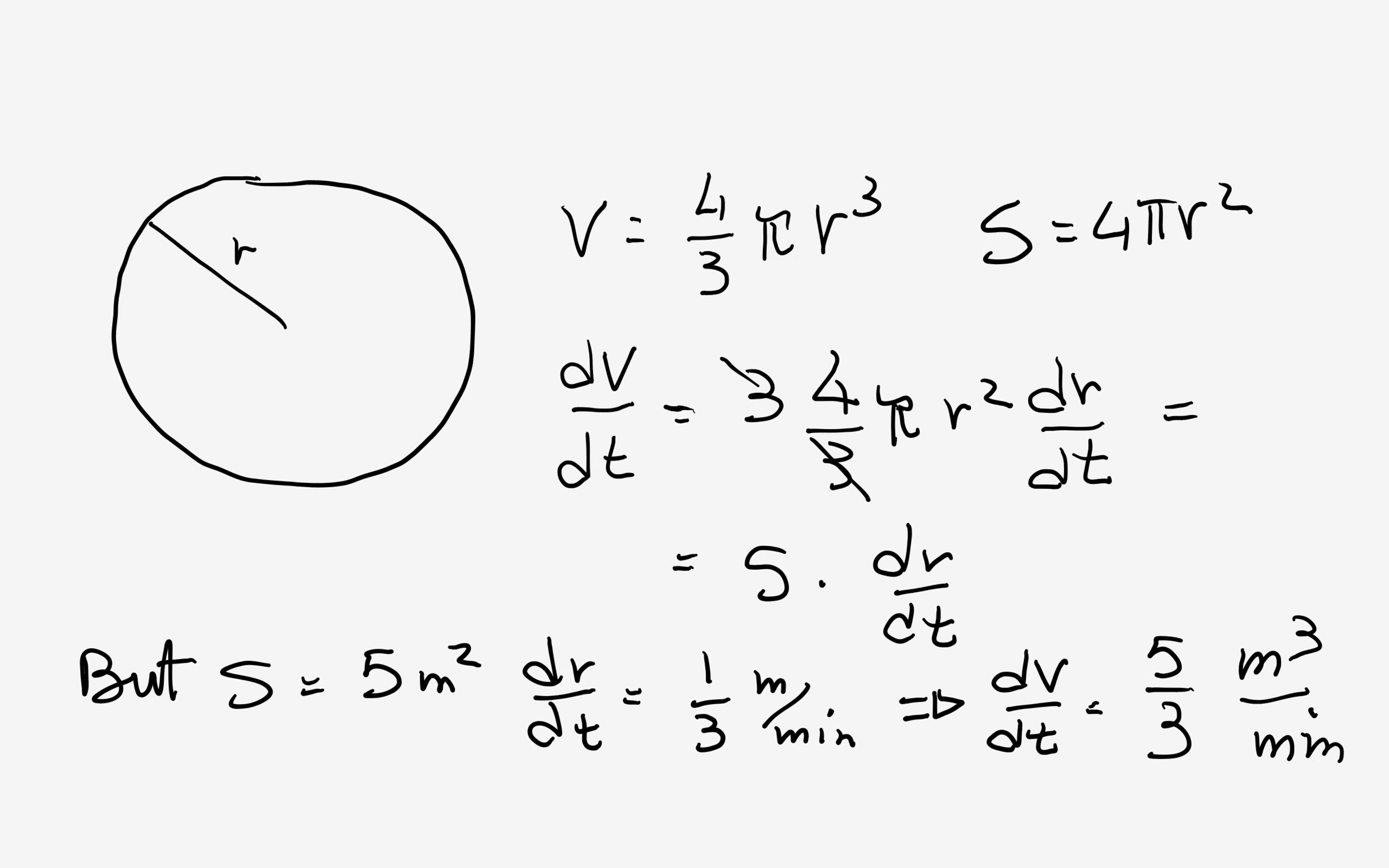Question

At what approximate rate (in cubic meters per minute) is the volume of a sphere changing at the instant when the surface area is 5 square meters and the radius is increasing at the rate of 1/3 meters per minute?

Answer 1

The volume of your sphere `V` is changing with time (and this reflects the fact the the radius is changing with time so affecting also the surface area `S`); rate of change in maths stands for derivative, `d/(dt)`, so try this: