B=20° C=75° b=5 solve the triangle?
When I set up the equation using law of sines it looked like this 5/sin(20)=x/sin(75)
then x=-2.124 what did I do wrong?
When I set up the equation using law of sines it looked like this 5/sin(20)=x/sin(75)
then x=-2.124 what did I do wrong?
1 Answer
Explanation:
You're calculator is in radians! That's why. It should be in degrees.
You are on the right track however!
Let's draw the triangle [Note: This is not to scale]:
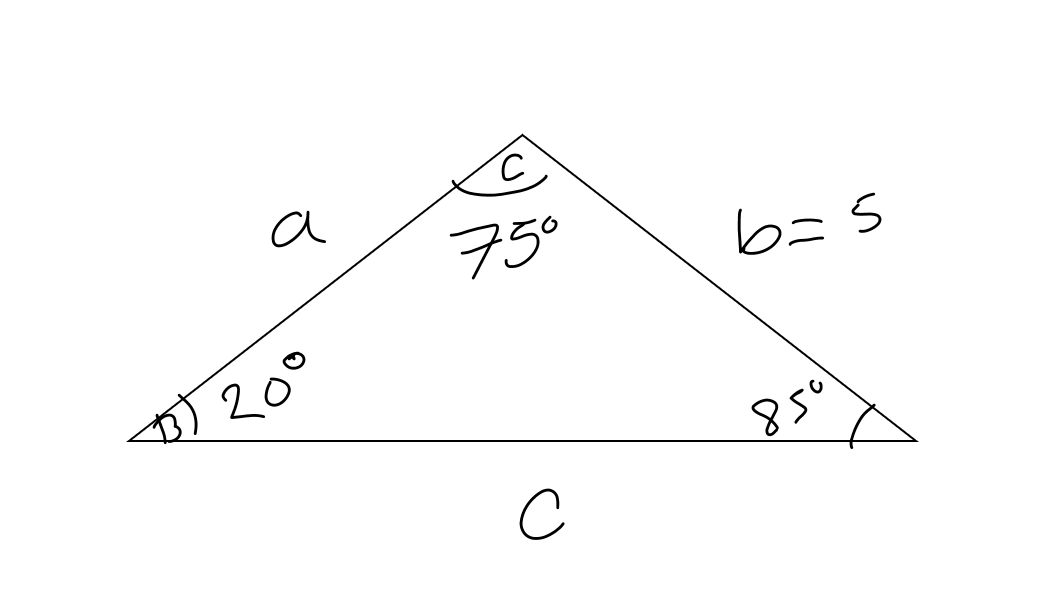
The missing angle can be found by knowing that the sum of the internal angles of any triangle is always equal to
So
The law of sines states:
We know:
What we want to know is
We can find the missing sides using the law of sines. So to find
Pluggin in what we know:
Similarly for

