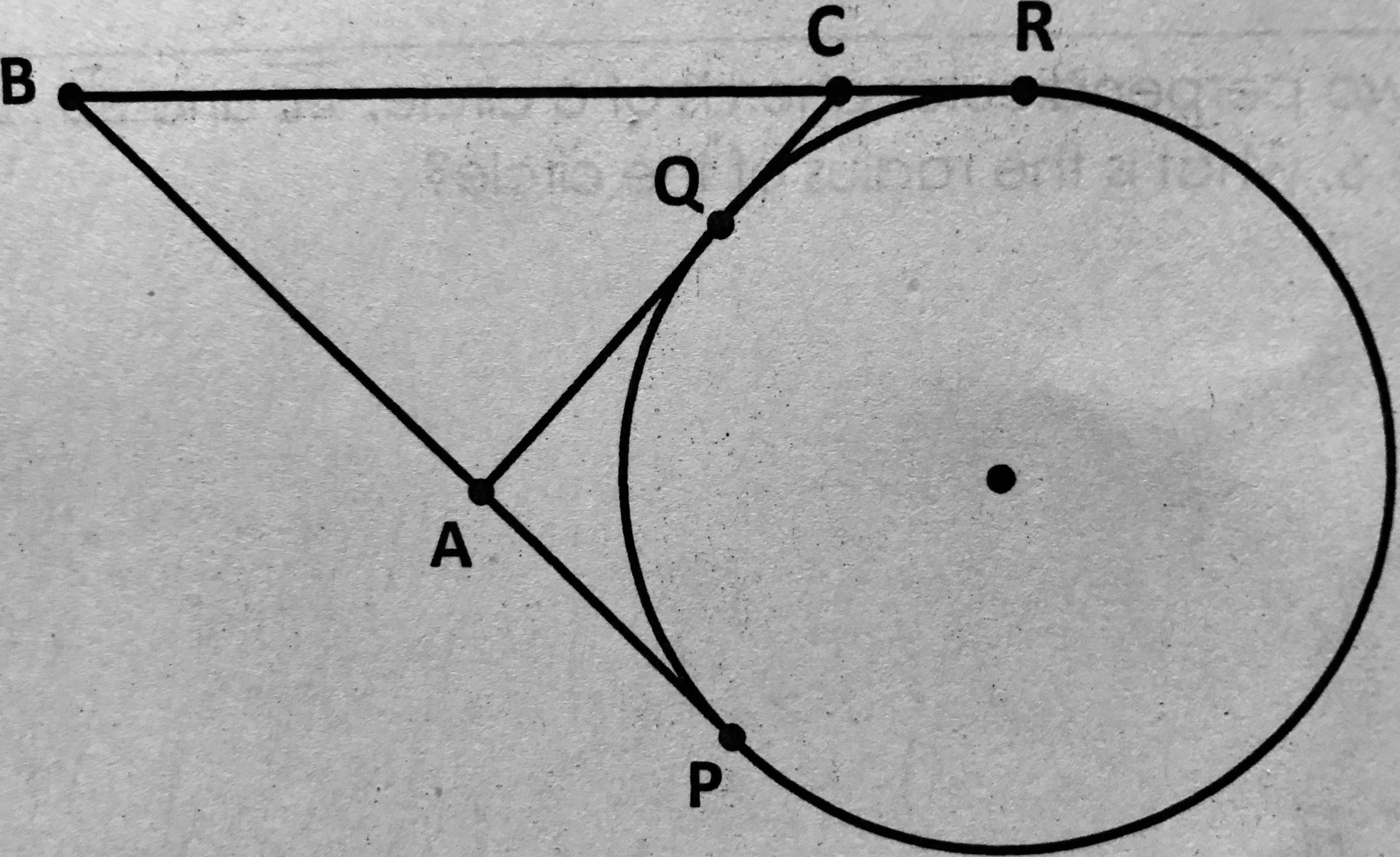
B is 34 mm from the center of circle O, which has a radius of 16 mm. Line BP and line BR are tangent segments. Line AC is tangent to circle O at point Q. Find the perimeter of ABC?
1 Answer
Oct 25, 2017
perimeter
Explanation:
as the two tangent segments to a circle from an external point are equal in length,
perimeter of
