Caesium has an atomic radius of #2.5 xx10^(-8)# cm and crystallizes in a body-centered cubic crystal structure . The length of the unit cell edge in picometers is?
1 Answer
Explanation:
All you have to do here is use the configuration of the unit cell for a body-centered cubic crustal structure and the radius of a cesium atom to help you find the diagonal of the unit cell.
Once you ahve the diagonal of the cell, you can use the Pythagorean Theorem to determine the length of the unit cell.
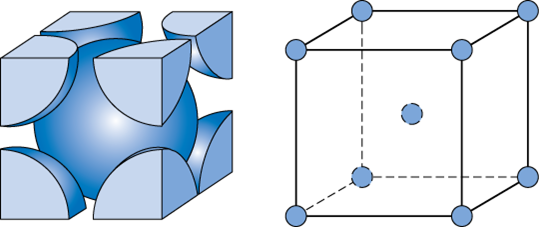
So, a body-centered cubic crystal structure is characterized by a total of
- one lattice point in every corner of the cube
- one lattice point in the center of the cube
To find the diagonal of the cell, pick a face of the cube and draw it as a square. You should end up with something like this
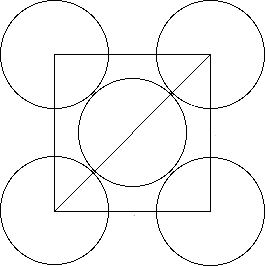
Now, let's say that
Using Pythagoras' Theorem, you can say that
#d^2 = x^2 + x^2#
#d^2 = 2x^2" " " "color(purple)((1))#
Now focus on writing the diagonal of the square by using
#r# , the radius of the top-right cesium atom#2r# , the diameter of the center atom#r# , the radius of the low-left cesium atom
The diagonal of the square will thus be
#d = r + 2r + r = 4r#
Plug this into equation
#(4r)^2 = 2x^2#
#16r^2 = 2x^2#
#8r^2 = x^2 implies x = sqrt(8r^2) = r * 2sqrt(2)#
You can find the length of the unit cell in centimeters, then convert it to picometers
#x = 2.5 * 10^(-8)"cm" * 2sqrt(2) = 7.1 * 10^(-8)"cm"#
As you know, you can use the following conversion factor
#"1 cm" = 10^(-2)"m" = 10^(-2) xx 10^(12)"pm" = 10^(10)"pm"#
This means that the edge length of the unit cell will be
#7.1 * 10^(-8)color(red)(cancel(color(black)("cm"))) * (10^(10)"pm")/(1color(red)(cancel(color(black)("cm")))) = color(green)("710 pm")#

