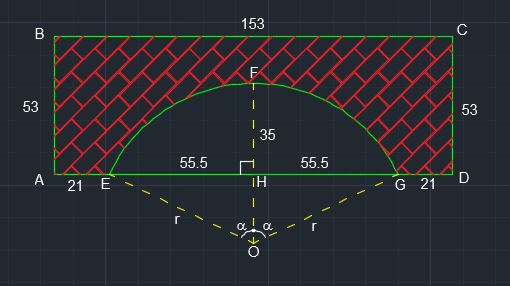
area of rectangle #ABCD=A_R=153xx53=8109.00 " m"^2#
let #O and r# be the center and the radius of arc #EFG#, respectively.
#r=OH+HF=OH+35#
#DeltaOHE# is a right triangle, by Pythagorean theorem, we get:
#r^2-OH^2=EH^2#
#=> (OH+35)^2-OH^2=55.5^2#
#=> OH^2+70*OH+35^2-OH^2=55^2#
#=> 70*OH+1225=3080.25#
#=> OH=(3080.25-1225)/70~~26.50# m
#=> r=OH+35=26.5+35=61.50# m
let #angleEOH=alpha#
#rsinalpha=55.5, => alpha=sin^-1((55.5)/(61.50))=64.4805^@#
#=> 2alpha=2*64.4805=128.961^@#
area of segment #EFG=A_S=pi*r^2*(2alpha)/(360)-1/2*r^2*sin2alpha#
#=r^2(pi*(2alpha)/360-(sin2alpha)/2)#
#=61.5^2(pi*128.961/360-sin128.961/2)#
#=2786.0 " m"^2#
Hence, area of the brick region #A_B=A_R-A_S#
#=8109.0-2786.0=5323.0 " m"^2#
