Question

Calculate the area of a small leaf?

At the right is the graph of the 8-leafed rose
`r = 1 + 2cos(4θ`).
Calculate the area of the small leaf.
As a check the answer is 0.136 to 3 places of decimal. (But of course you have to calculate the exact answer.)
[Techhelp: `int__ cos^2(k theta)d theta=1/2theta+1/(4k)sin(2k theta)+C`

Answer 1

Area of one small leaf `=0.34243`

Area of all four small leaves `=1.36971`

Explanation:

.

`r=1+2cos(4theta)`

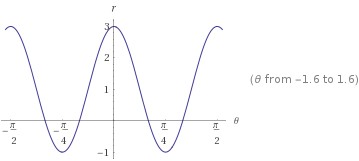
We will graph this function in cartesian and polar coordinates to learn more about its behavior. In cartesian coordinate system, we will make the `x`-axis the `theta`-axis and the `y`-axis the `r`-axis.

Let's set the function equal to `0` and solve for its `theta`-intercepts.

`1+2cos(4theta)=0`

`2cos(4theta)=-1`

`cos(4theta)=-1/2`

`4theta=arccos(-1/2)`

`4theta=(-10pi)/3, (-8pi)/3, (-4pi)/3, (-2pi)/3, (2pi)/3, (4pi)/3, (8pi)/3, (10pi)/3`

`theta=(-5pi)/6, (-2pi)/3, (-pi)/3, (-pi)/6, pi/6, pi/3, (2pi)/3, (5pi)/6`

Plugging values of `theta` that are in between each two values above, allows us to identify additional points on the graph and make the shape of the graph clearer.

The cartesian graph of the function is:

The polar graph of it is:

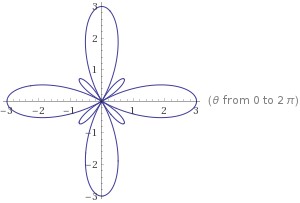
Additionally, it shows us that, in the cartesian coordinate system, values of `theta` between `(-pi)/6 and pi/6` result in one large area between the curve and the `theta`-axis. In the polar coordinate system, this results in an enclosed area in one large leaf.

The cartesian graph of this area is:

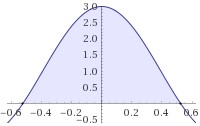
The polar graph of this area is:

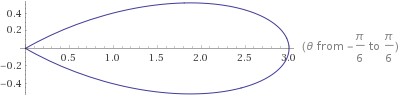
Similarly, in the cartesian coordinate system, values of `theta` that are in between `(-2pi)/3 and (-5pi)/6` result in one small area between the curve and the `theta`-axis. In the polar coordinate system, this results in an enclosed area in one small leaf.

The cartesian graph of this area is:

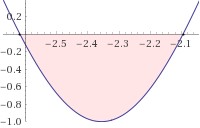
The polar graph of this area is:

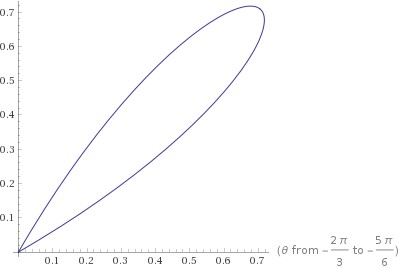
The eight `theta` values indicated above, are in fact four sets of two `theta` values that are the boundaries of these leafs alternating between large and small leaves.

To find the area of one small leaf, we will take the integral of the function and evaluate it between `(-2pi)/3 and (-5pi)/6`.

`int_((-2pi)/3)^((-5pi)/6)(1+2cos(4theta))d theta=`

`int_((-2pi)/3)^((-5pi)/6)d theta + 2int_((-2pi)/3)^((-5pi)/6)cos(4theta)d theta=theta+2I)_((-2pi)/3)^((-5pi)/6)`

`I=intcos(4theta)d theta`

Let `z=4theta, :. dz=4d theta, :. d theta=(dz)/4`

Let's substitute:

`I=1/4intcoszdz=1/4sinz=1/4sin(4theta)`

`int_((-2pi)/3)^((-5pi)/6)(1+2cos(4theta))d theta=theta+1/2sin(4theta))_((-2pi)/3)^((-5pi)/6)=`

`(-5pi)/6+1/2sin((-10pi)/3)-[(-2pi)/3+1/2sin((-8pi)/3)]=`

`(-5pi)/6+1/2(sqrt3/2)+(2pi)/3-1/2(-sqrt3/2)=`

`(-pi)/6+sqrt3/2=0.34243`

Area of one small leaf `=0.34243`

Area of all four small leaves `=1.36971`