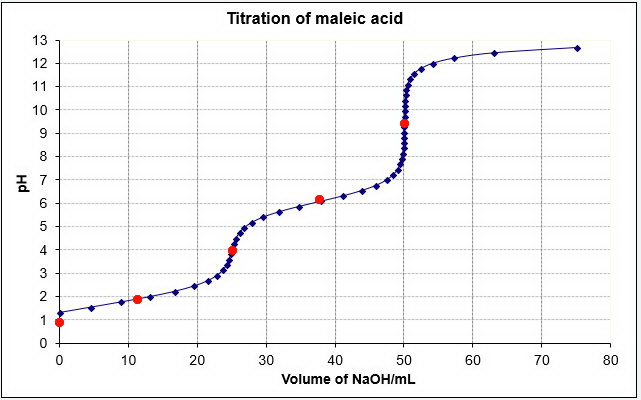
You are titrating a dibasic acid. The equilibria involved are
#"H"_2"A" + "H"_2"O" ⇌ "HA"^"-" + "H"_3"O"^"+"; K_text(a₁) = 1.48 × 10^"-2"; "p"K_text(a₁) = 1.83#
#"HA"^"-" + "H"_2"O" ⇌ "A"^"2-" + "H"_3"O"^"+"; color(white)(ll)K_text(a₂) = 8.51 × 10^"-7"; "p"K_text(a₂) = 6.07#
a) At 0 mL
#color(white)(mmmmmm)"H"_2"A" + "H"_2"O" ⇌ "HA"^"-" + "H"_3"O"^"+"#
#"I/mol·L"^"-1":color(white)(m)0.2color(white)(mmmmmmll)0color(white)(mmml)0#
#"C/mol·L"^"-1":color(white)(m)"-"xcolor(white)(mmmmmml)"+"xcolor(white)(mm)"+"x#
#"E/mol·L"^"-1":color(white)(l)"0.2 -" xcolor(white)(mmmmmm)xcolor(white)(mmm)x#
#K_"a" = (["H"_3"O"^+]["A"^"-"])/(["HA"]) = x^2/(0.2-x) = 1.48 × 10^"-2"#
Check for negligibility
#0.2/(1.48 × 10^"-2") = 13 < 400#. ∴ We must solve a quadratic.
#x^2 = (0.2-x) × 0.0148 = 0.0296 - 0.0148x#
#x^2 + 0.0148x - 0.0296 = 0#
#x = 0.165#
#["H"_3"O"^"+"] = xcolor(white)(l) "mol/L" = "0.165 mol/L"#
#"pH" = -log["H"_3"O"^"+"] = -log0.165 = 0.78#
b) At 12 mL
#"Initial moles of acid" = 25 color(red)(cancel(color(black)("mL H"_2"A"))) × ("0.2 mmol H"_2"A")/(1 color(red)(cancel(color(black)("mL H"_2"A")))) = "5.0 mmol H"_2"A"#
#"Moles of NaOH added" = 12color(red)(cancel(color(black)("mL NaOH"))) × ("0.2 mmol NaOH")/(1 color(red)(cancel(color(black)("mL NaOH")))) = "2.4 mmol NaOH"#
#color(white)(mmmmmm)"H"_2"A" + "OH"^"-" ⇌ "HA"^"-" + "H"_2"O"#
#"I/mmol":color(white)(mll)50color(white)(mmll)24color(white)(mmml)0#
#"C/mmol":color(white)(m)"-24"color(white)(mml)"-24"color(white)(mm)"+24"#
#"E/mmol":color(white)(ml)26color(white)(mmm)0color(white)(mmml)24#
#"pH = p"K_text(a₁) + log((["HA"^"-"])/(["H"_2"A"])) = 1.83 + log(24/26) = 1.83 - 0.0348 = 1.79#
c) At 25 mL
#"Moles of NaOH added" = 25color(red)(cancel(color(black)("mL NaOH"))) × ("0.2 mmol NaOH")/(1 color(red)(cancel(color(black)("mL NaOH")))) = "50 mmol NaOH"#
You have neutralized all the #"H"_2"A"#. You are at the first equivalence point.
#"pH" = 1/2("p"K_text(a₁) + "p"K_text(a₂)) = 1/2(1.83 + 6.07) = 7.90/2 =3.95#
d) At 37.5 mL
#"Moles of NaOH added" = 37.5color(red)(cancel(color(black)("mL NaOH"))) × ("0.2 mmol NaOH")/(1 color(red)(cancel(color(black)("mL NaOH")))) = "7.5 mmol NaOH"#
You have neutralized all the #"H"_2"A"# and half the #"HA"^"-"#.
Thus,
#"pH = p"K_text(a₂) = 6.07#
e) At 50 mL
#"Moles of NaOH added" = 50color(red)(cancel(color(black)("mL NaOH"))) × ("0.2 mmol NaOH")/(1 color(red)(cancel(color(black)("mL NaOH")))) = "10 mmol NaOH"#
You have neutralized all the #"H"_2"A"# and all the #"HA"^"-"#.
You have a solution of 5.0 mmol of #"A"^"2-"# in 75 mL.
#["A"^"-"] = "5.0 mmol"/"75 mL" = "0.067 mol/L"#
#color(white)(mmmmmm)"A"^"2-" +color(white)(m) "H"_2"O"color(white)(m) ⇌ color(white)(m)"HA"^"-" + "OH"^"-"#
#"I/mol":color(white)(mll)0.067color(white)(mmmmmmmmm)0color(white)(mmm)0#
#"C/mol":color(white)(mm)"-"xcolor(white)(mmmmmmmmml)"+"xcolor(white)(mm)"+"x#
#"E/mol":color(white)(m)"0.067-"xcolor(white)(mmmmmmmml)xcolor(white)(mmll)x#
#K_"b" = K_"w"/K_"a₂" = (1.00 × 10^"-14")/(8.51 × 10^"-7") = 1.18 × 10^"-8"#
#K_"b" = (["HA"^"-"]["OH"^"-"])/(["A"^"2-"]) = x^2/(0.067-x) = 1.18 × 10^"-8"#
Check for negligibility
#0.067/(1.18 ×10^"-8") = 5.7 × 10^"-6" > 400#. ∴ #x ≪ 0.067#
#x^2 = 0.067 × 1.18 × 10^"-8" = 7.8 × 10^"-10"#
#x = sqrt(7.8 × 10^"-10") = 2.8 × 10^"-5"#
#["OH"^"-"] = 2.8 × 10^"-5" color(white)(l)"mol/L"#
#"pOH" = -log(2.8 × 10^"-5") = 4.55#
#"pH = 14.00 - pOH = 14.00 - 4.55 = 9.45"#
Your calculated values should match the red dots in the titration curve below.