Calculate the wavelength of Radio 4 which broadcasts on a frequency of "198 kHz" ?
1 Answer
Explanation:
The thing to remember about wavelength and frequency is that they have an inverse relationship given by the equation
color(blue)(ul(color(black)(lamda * nu = c))
Here
lamda is the wavelength of the wavenu is its frequencyc is the speed of light, usually taken to be in a vacuum, i.e.c = 3 * 10^8 \ "m s"^(-1)
This basically tells you that if you multiply the wavelength and the frequency, you must always end up with the value of the speed of light,
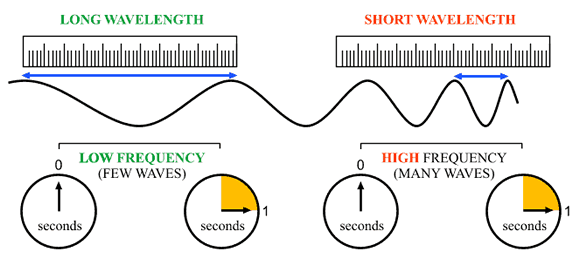
In your case, you already know the frequency of the radio waves
"198 kHz" = 198 color(red)(cancel(color(black)("kHz"))) * (10^3 \ "Hz")/(1color(red)(cancel(color(black)("kHz")))) = 1.98 * 10^5 \ "Hz"
As you know, you have
"1 Hz" = "1 s"^(-1)
which means that the frequency of the radio waves can be written as
1.98 * 10^5 \ "Hz" = 1.98 * 10^5 \ "s"^(-1)
Since no information was given about the value of the speed of light, you can assume that you're working with the approximation
c = 3 * 10^8 \ "m s"^(-1)
Rearrange the equation to solve for
lamda * nu = c implies lamda = c/nu
Plug in your values to find
lamda = (3 * 10^8 \ "m"color(red)(cancel(color(black)("s"^(-1)))))/(1.98 * 10^5 color(red)(cancel(color(black)("s"^(-1))))) = color(darkgreen)(ul(color(black)(1.51 * 10^3 \ "m")))
The answer is rounded to three sig figs, the number of sig figs you have for the frequency of the radio waves.

