when #x = 9#, #x - 9 = 0#
when #x = 9#, #f(x) = (9-9)/(9-9)#
#= 0/0#
any number divided by #0# is undefined, so there is a discontinuity in the graph of #f(x) = (|x-9|)/(x-9)#, at #x = 9#.
this is what the entire graph looks like:
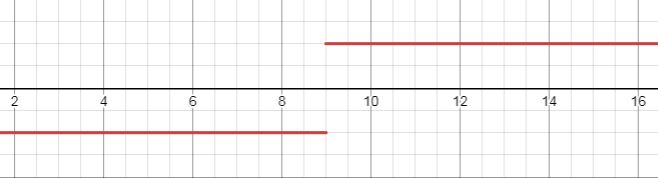
when #x < 9#, #x-9 < 0#
#|x - 9|# is always greater than #0# since it is an absolute value, meaning that dividing it by a negative number will give a negative number.
when #x - 9# is negative, #|x - 9|# is the additive inverse, and so dividing the two will give #1/-1#, or #-1#.
that is why, for all values of #x# below #9#, #f(x) = -1#.
when #x - 9# is positive, #|x - 9|# is the same number, and so dividing the two will give #1/1#, or #1#.
that is why, for all values of #x# above #9#, #f(x) = 1#.

