Can an ordinary least squares regression be used with time-series data?
1 Answer
Mar 3, 2016
Yes.
Explanation:
Least-squares regression is as applicable to time-series data as it is to data which is dependent on any other variable. One can use least-squares to find a best fit of a function of time to data gathered in a time series.
For example, imagine a pendulum swinging back a forth, and a measurement apparatus which gathers data on the position of the pendulum. This data has a time,
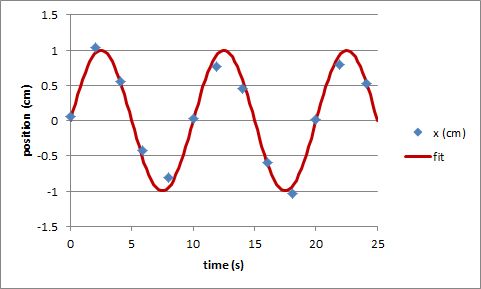
We can use a least-squares approach to determine the coefficients of a fit function, in this case we may be using the following function:
Where we adjust the coefficients

