Can anybody please solve it?
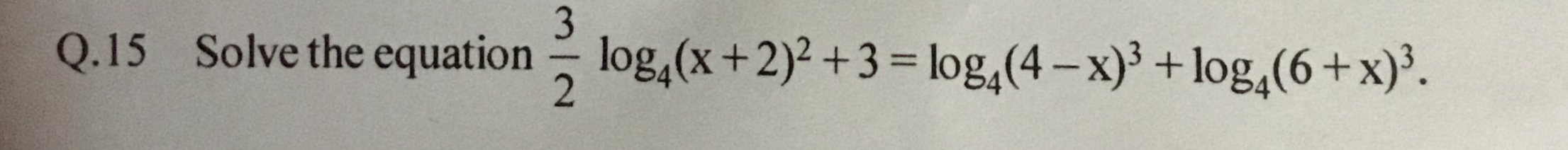
answers are x=2 or #1-root2 33#
I got x=2 but did not get x=#1-root2 33#
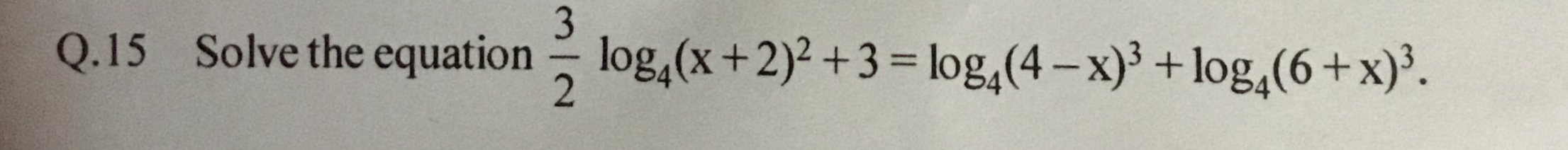
answers are x=2 or
I got x=2 but did not get x=
2 Answers
Explanation:
Use
Dividing both sides by 3,
Using
Use
If we look at the original equation, there's no problem plugging in 2, but if we plug in
Therefore, the only acceptable solution is
Explanation:
Since we are taking the power down, we have to consider absolute values. For even exponents, we need them, hence
Assuming
As stated above, the
Assuming
Since
The limiting condition is that we need to take the logarithm of
So the other solution is

