Can anyone confirm the answer I have to this question?

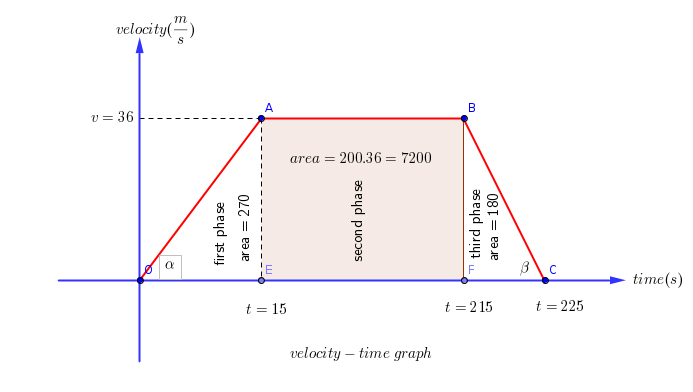
Total time: 225 sec
Total distance travelled: 8100 m
Speed: 36 m/s
Total time: 225 sec
Total distance travelled: 8100 m
Speed: 36 m/s
2 Answers
Given
For first phase journey
So applying kinematic equation
we get distance traversed in first phase
For Second phase journey
At the end first phase it will acquire velocity
So
This journey occurs at constant velocity
So distance traversed in this phase
For third phase journey
So
Distance traversed in 3rd phase
So total duration
Total distance traversed
So average speed
Explanation: