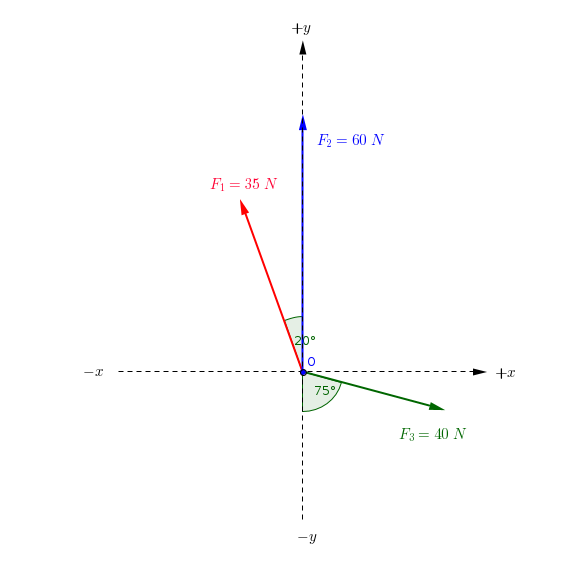
#"all forces acting on object"#
#".................................................................................................."#
#"The Force "F_1" and its components(vertical,horizontal)"#
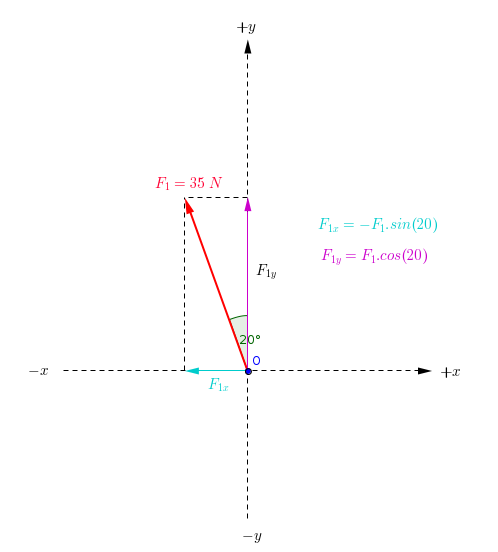
#F_("1x")=-F_1.sin(20)=-35.0,34202014=-11.97" N"#
#F_("1y")=F_1.cos(20)=35.0,93969262=32.89" N"#
#"...................................................................................."#
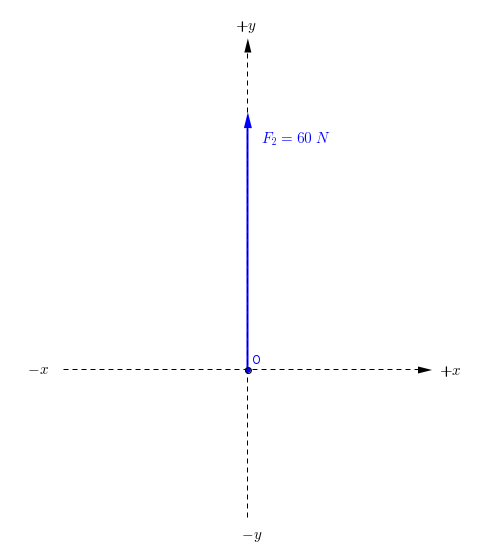
#"The Force "F_2" and its components(vertical,horizontal)"#
#"The Force "F_2 " has vertical component only ."#
#F_("2x")=0#
#F_("2y")=60" N"#
#"...................................................................................................."#
#"The Force "F_3" and its components(vertical,horizontal)"#
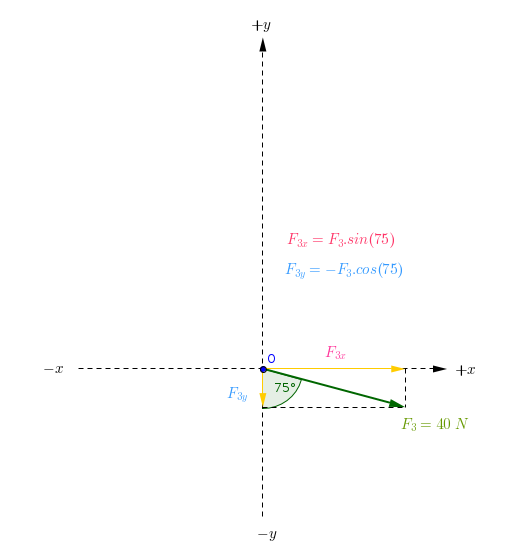
#F_("3x")=F_3.sin(75)=40.0,96592583=38.64" N "#
#F_("3y")=-F_3.cos(75)=-40.0,25881905=-10.35" N"#
#.....................................................................................................#
#"now let us find the total "F_x" and "F_ y " components."#
#F_x=F_("1x")+F_("2x")+F_("3x")#
#F_y=F_("1y")+F_("2y")+F_("3y")#
#F_x=-11.97+0+38.64=26.67" N"#
#F_y=32.89+60-10.35=82.54" N"#
#".................................................................................."#
#"Resultant Vector..."#
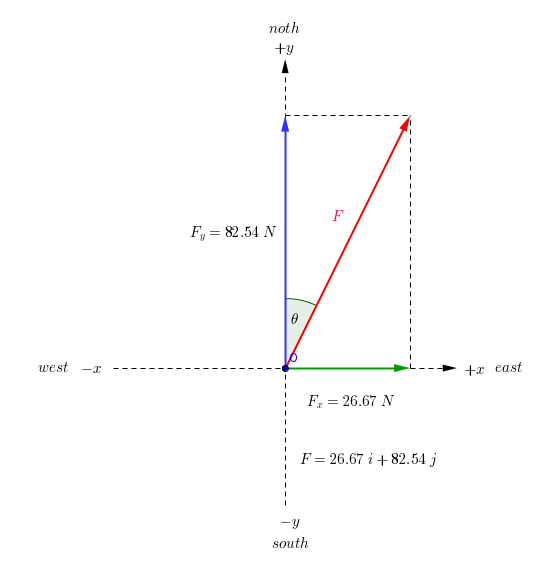
#" magnitude of the resultant vector can be calculated :"#
#F=sqrt((F_x)^2+(F_y)^2)#
#F=sqrt((26.67)^2+(82.54)^2)#
#F=sqrt(711.2889+6812.8516)#
#F=sqrt(7524.1405)#
#F=86.74" N"#
#"we must find " tan(theta) " for direction of the resultant vector."#
#tan(theta)=(F_x)/(F_y)#
#tan(theta)=(26.67)/(82.54)#
#tan(theta)=0.32311606#
#theta=17.91 #







