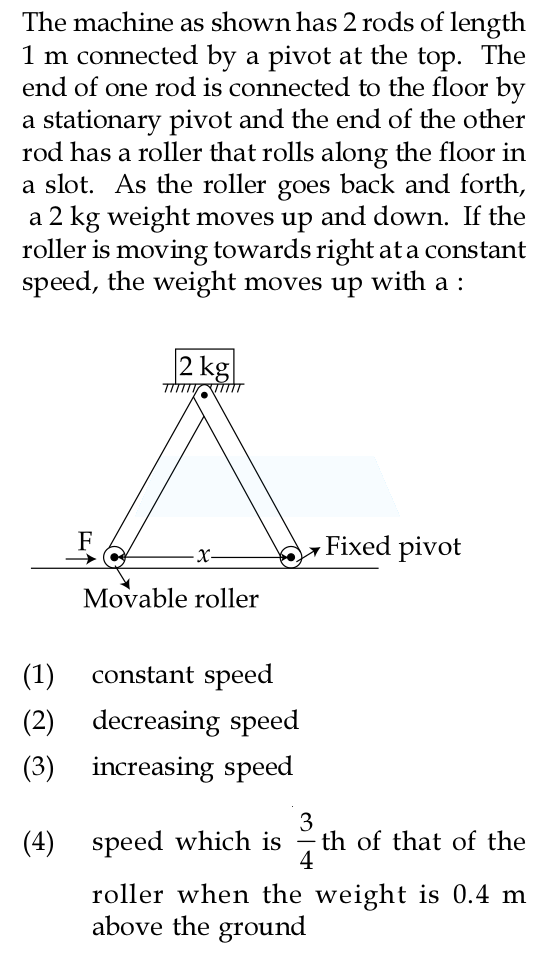
Let the height of the weight be #y#. Then it is easy to see that
#y^2+(x/2)^2 = l^2#
where #l=1" m"# is the length of each rod.
Differentiating, we get
#2y (dy)/(dt) + 1/4 2 x (dx)/(dt) = 0#
Thus
#dy/dt = -1/4 x/y dx/dt#
In the problem, if we choose the stationary pivot as the origin and the #X# axis towards the left, then #x>0# and #dx/dt<0#, So
#dy/dt = 1/4 x/y |dx/dt|#
It is stated that #dx/dt# is a constant. On top of this, #x# is decreasing while #y# is increasing. So#x/y# is decreasing with times - and thus the weight is moving up with decreasing speed.
When #y# is 0.4 m , we can see that
#(x/2)^2 = l^2-y^2 = (1^2-0.4^2)" m"^2 = 0.84" m"^2#
Thus #x = 0.92# m, and these values say that
#dy/dt = 1/4 0.92/0.4 |dx/dt| ~~0.57|dx/dt|#