Can I get some help please? Thanks
3 Answers
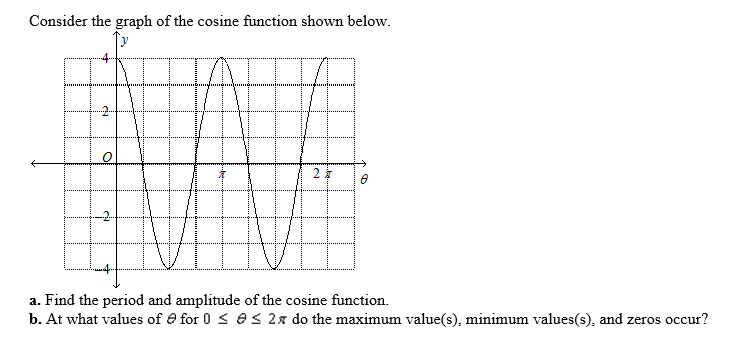
Part a.
Please observe that the cosine function starts at the value of 4 at
and then repeats the value of 4:
Therefore, the period must be
We can double-check this by observing that it repeats the value of 4, again,
Because the value of the function varies between 4 and -4, the amplitude must be 4.
End part a.
Part b.
By observation:
The maximum values occur at
The minimum values occur at
The zeros occur at
Explanation:
#• " Amplitude is the distance from the "theta" axis to the"#
#"peak of the wave"#
#"from the origin "O to 4#
#rArr"amplitude "=4#
#• " period is the distance covered by 1 complete wave"#
#"from 1 point on the wave to the same point along the wave"#
#rArr"period "=pi#
#"maximum values of + 4 at "theta=0,theta=pi,theta=2pi#
#"minimum values of - 4 at "theta=pi/2,theta=(3pi)/2#
#color(blue)"zeros"" are where the wave intersects the "theta" axis"#
#"zeros occur at "theta=pi/4,theta=(3pi)/4,theta=(5pi)/4,theta=(7pi)/4#
See below.
Explanation:
a.) The period is the distance from one peak to the next peak, or from one trough to the next trough. From the graph this can be seen as being from
So the period is
The amplitude is the distance from the horizontal axis to the top of a peak. From the graph this can be seen as 4:
So amplitude is 4:
b.)
Maximum value of 4 between
Minimum value -4 between
The zeros occur where the curve cuts the horizontal axis. From graph these can be seen to occur at:

