This strange behavior can be depicted by considering
#f_(n-1)(x)=sum_(k=0)^(n-1) sin(kx) = 1/(2i)sum_(k=0)^(n-1) e^(ikx)-1/(2i) sum_(k=0)^(n-1) e^(-ikx) = 1/(2i)( (e^(i nx)-1)/(e^(ix)-1)-(e^(-i nx)-1)/(e^(-ix)-1))=(cos(x/2)-cos(x/2-nx))/(2cos(x/2))#
Now by solving
#(df_(n-1))/(dx) = ( n Cos(x - n x)-1 - (n-1) Cos(n x)) /sin^2(x/2) = 0#
we can determine the relative minima/maxima and then produce an approximate plot of such behavior.
Note that #lim_(n->oo) f_(n-1)(x) = sum_(k=0)^oo sin(kx)#
Attached a plot for #n = 10#
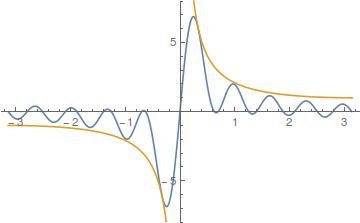
NOTE
We were using the so called de Moivre's identity
#e^(ix) = cos x +i sin x# and consequently
#sinx = 1/(2i)(e^(ix)-e^(-ix))#
We were using also the polynomial identity
#(x^(n+1)-1)/(x-1) = sum_(k=0)^n x^k#
Also, to get #(cos(x/2)-cos(x/2-nx))/(2cos(x/2))# we proceed as follows.
#(e^(n i x) - 1) (e^(-i x) - 1) - (e^(-n i x) - 1) (e^(i x) - 1)=e^(ix)-e^(-ix) -(e^(i nx)-e^(-i nx))-(e^(i(1-n)x)-e^(-i(1-n)x))# and
#(e^(i x) - 1) (e^(-i x) - 1) = 2(1-cosx)#
etc.
It is left as an exercise:
for #0 < x < pi, n in NN#
#(cos(x/2)-cos(x/2-nx))/cos(x/2) le Tan(x/4) - Tan(x/4 - pi/2)#


