Can someone help clarify this question?
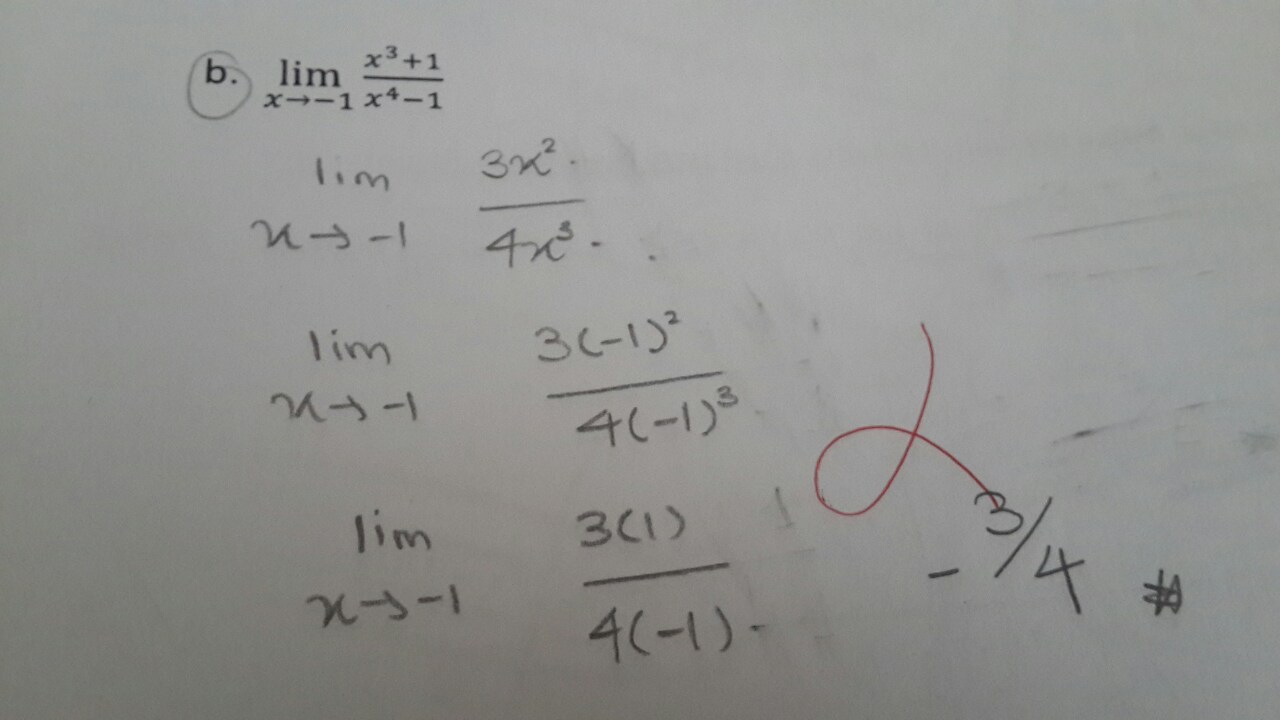
1 Answer
Feb 24, 2017
You have followed L'Hospital's Rule and nothing wrong in it.
Probably you are not permitted to follow this rule. You can ask your teacher whether it is permissible or not.
Otherwise you can proceed as shown below. I think this is also known to you .

