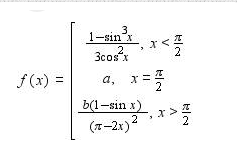To find the left hand limit #lim_{x to (pi/2)^-} f(x)# we note that for #x<pi/2#
#f(x) = (1-sin^3x)/(3cos^2x) #
# = ((1-sin x)(1+sin x+sin^2x))/(3(1-sin x)(1+sin x))#
# = (1+sin x+sin^2x)/(3(1+sin x)) #
where the last step is legitimate as one approaches #pi/2# because #(1-sin x)# is non-zero as long as #x ne pi/2#
Thus
#lim_{x to (pi/2)^-} f(x) = lim_{x to pi/2} (1+sin x+sin^2x)/(3(1+sin x))=1/2#
Hence for continuity, we have
#color(red)(a = 1/2)#
To figure out the right hand limit we use
#(b(1-sinx))/(pi-2x)^2 #
#= b/16(sin^2(x/2)+cos^2(x/2)-2 sin(x/2)cos(x/2))/(x/2-pi/4)^2#
# = b/16 (sin(x/2)-cos(x/2))^2/(x/2-pi/4)^2#
# = b/8 (sin(x/2)1/sqrt2-cos(x/2)1/sqrt2)^2/(x/2-pi/4)^2#
# = b/8 (sin(x/2)cos(pi/4)-cos(x/2)sin(pi/4))^2/(x/2-pi/4)^2#
# = b/8 sin^2(x/2-pi/4)/(x/2-pi/4)^2#
Hence the right hand limit is
# lim_{x to (pi/2)^+} f(x) = lim_{x to (pi/2)} b/8 sin^2(x/2-pi/4)/(x/2-pi/4)^2 #
#qquad = b/8 lim_{(x/2-pi/4) to 0} (sin(x/2-pi/4)/(x/2-pi/4))^2 = b/8#
Thus for #f(x)# to be continuous, we must also have
#b/8 = 1/2 implies color(red)( b=4)#