Can someone help me with geometry?
∠E = 40. In addition, the arches AB, BC and CD are equal to each other. Find ∠ACD. I'm struggling in general with geometry. Could someone help me with this task? In general when given a figure to analyze what is the first things you look for? I struggle mostly with analyzing a figure and finding information and wonder if someone have any bulletpoints or advices so it gets easier to find information?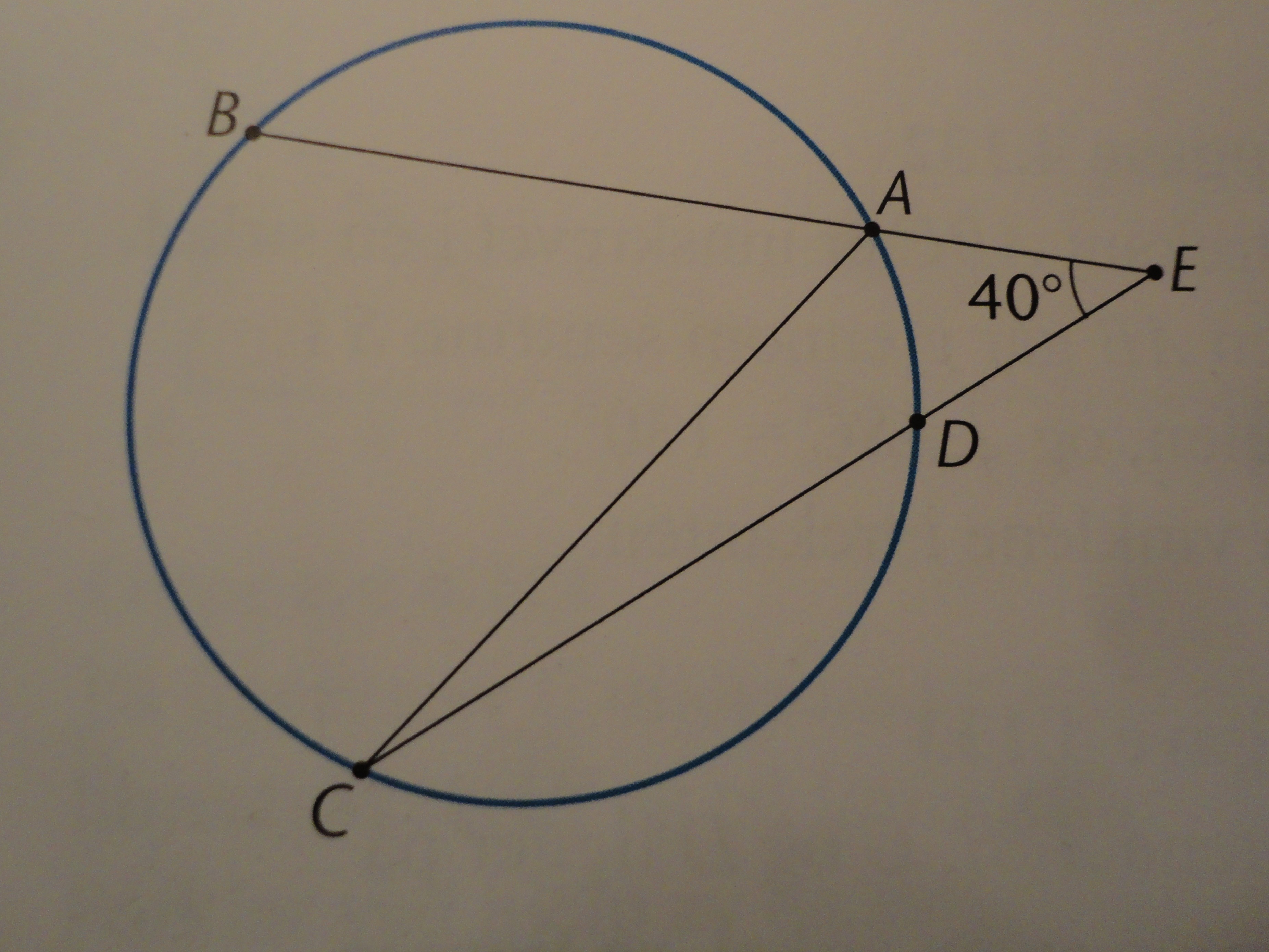 Really appreciate help :)
Really appreciate help :)
∠E = 40. In addition, the arches AB, BC and CD are equal to each other. Find ∠ACD. I'm struggling in general with geometry. Could someone help me with this task? In general when given a figure to analyze what is the first things you look for? I struggle mostly with analyzing a figure and finding information and wonder if someone have any bulletpoints or advices so it gets easier to find information? Really appreciate help :)
2 Answers
I got 15 degrees
Explanation:
First off, I would label the diagram with the given information and draw a dotted line from point B to point C. Label the congruent arcs. The segments that intercept the arcs- segments AB, BC, and CD are congruent due to the inverse of the chord arcs conjecture.
The conjecture states that if two chords in a circle are congruent, then their intercepted arcs are congruent.
Since the segments BA and CD are congruent, that means segments BE and CE are congruent as well because of the tangent segments conjecture. The conjecture states that tangent segments to a circle from a point outside the circle are congruent.
The triangle BCE is an isosceles triangle. That means both angles ABC and BCE are 70 degrees (they are the base angles, which are congruent in isosceles triangles), because the third angle (the vertex angle) is 40 degrees in your problem.
That means your answer must be smaller than 70 degrees.
Another isosceles triangle can be formed. That triangle would be BAC because the problem tells us that segments BA and BC are congruent. We already know that angle ABC is 70 degrees. It is the vertex angle because the two congruent sides of the isosceles triangle form it. That means angles BCA and BAC are congruent. They are both 55 degrees because a triangle must add up to 180 degrees.
Angles BCA (55 degrees) and ACD (your answer) make up the larger angle, angle BCE (70 degrees). Subtract the 55 degrees from the 70 degrees to find ACD.
I hope I didn't confuse you too much, and I'm sure there are easier ways to do this problem, but that was the first way that I saw. In general just look at different shapes that you can create and never disregard any information that they provide to you.
Explanation:
.
There is a theorem called the Inscribed Angle Theorem that says the measure of an inscribed angle (an angle whose vertex is on the circumference of the circle) is equal to half the measure of the arc it is facing. This means:
This angle is also the exterior angle to the triangle
We also know that:
because they are equal to one time around the circle. But the problem statement says that
From(Equation 1):
Also because
We set these two equations equal to each other:
We plug in measure of
The answer to your question for a blueprint to finding information is that you need to go over the theorems about various types of angles in and around circles and understand them. Once you do that you can spot the information you are looking for in a given problem or figure.


