Can someone help prove this statement?

Let E be the center of AB in the triangle ABC. Furthermore, A is the center of DC, and line BD hits line through C and E in F.

Show that F shares the line DB in the 2: 1 ratio.
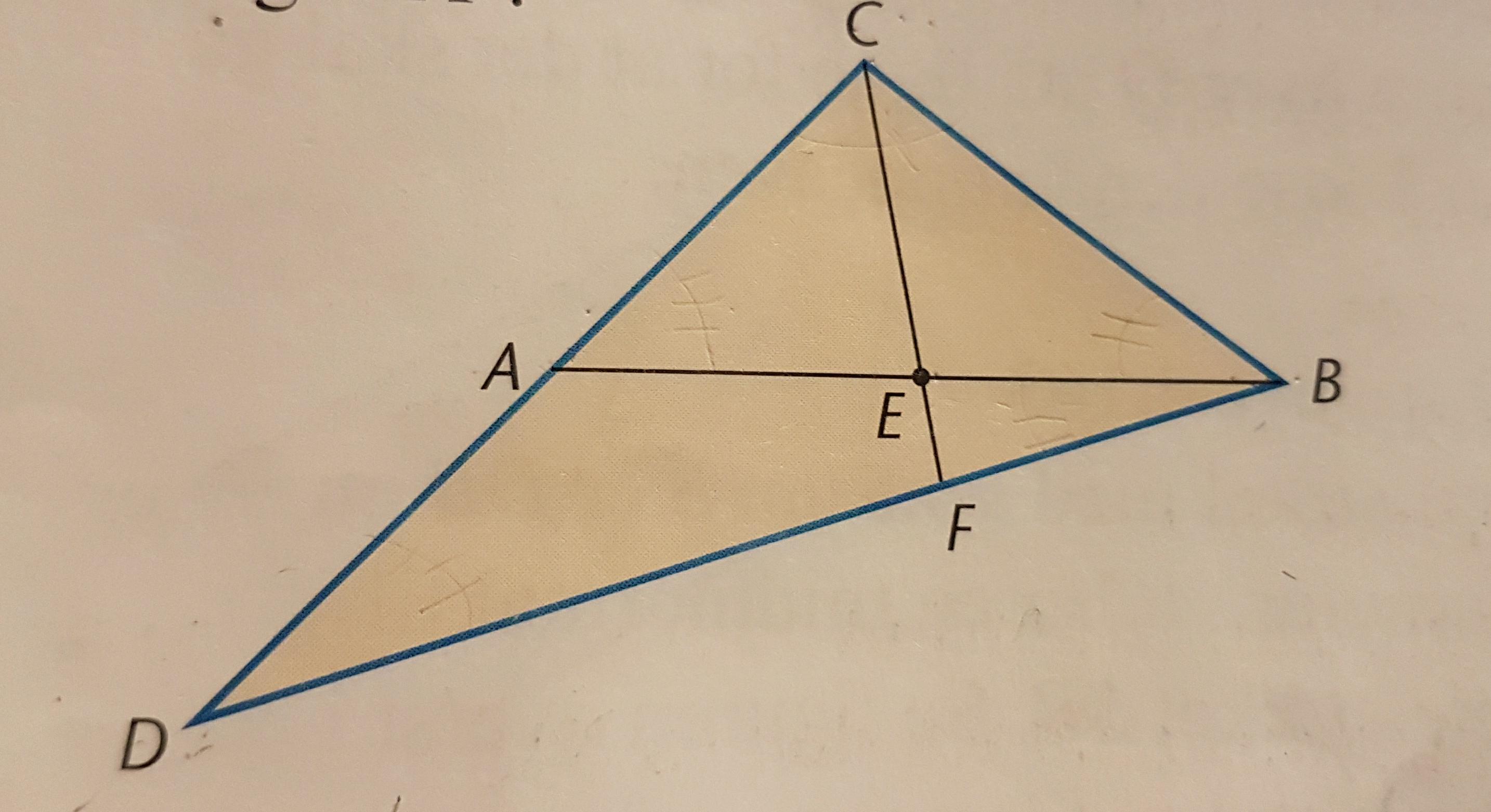
enter image source here

1 Answer
CW
Jan 16, 2018

see explanation.

Explanation:

enter image source here
Draw a line #AG#, parallel to #CF#, as shown in the figure,
#=> DeltaBEF and DeltaBAG# are similar,
as #AE=EB, => GF=FB#,
#DeltaDAG and DeltaDCF# are similar,
similarly, as #DA=AC, => DG=GF#,
#=> DG=GF=FB or DG:GF:FB=1:1:1#,
#=> DF:FB=(DG+GF):FB=2:1#

Related questions
Impact of this question
915 views around the world
You can reuse this answer
Creative Commons License