Can You Explain The Golden Ratio?
1 Answer
A few observations...
Explanation:
The golden ratio is supposed to be an optimally visually pleasing ratio for a rectangle.
In fact it is the ratio of the sides of a rectangle such that when a square is removed from one end, the remaining rectangle is in the same proportions.
A golden rectangle (so called) can be approximated by reversing this process, starting with a small square and attaching squares in a spiral arrangement, like this:
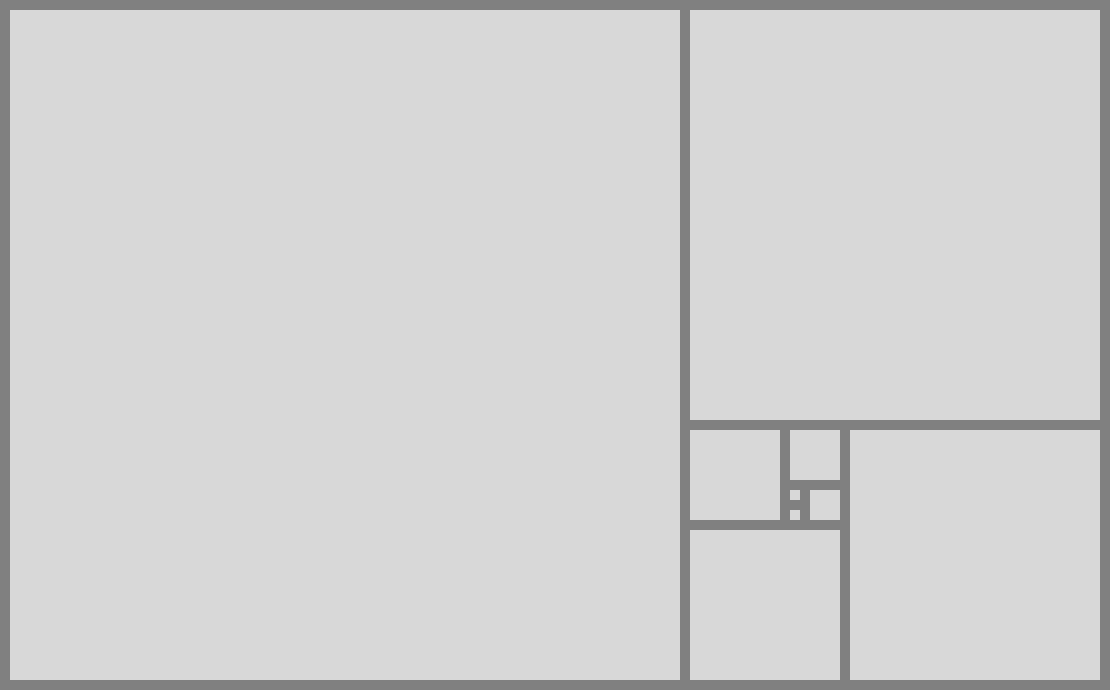
If the smallest square is of side
1, 1, 2, 3, 5, 8, 13, 21, 34,...
where each term is the sum of the previous two terms.
This sequence is called the Fibonacci sequence.
The ratio of the larger side to the smaller is therefore given by the continued fraction:
[1;bar(1)] = 1+1/(1+1/(1+1/(1+1/(1+1/(1+...)))))
We can evaluate this by solving:
x^2-x-1 = 0
to find
This value crops up so much that it is given its own Greek letter
Three golden rectangles arranged perpendicularly to one another have vertices that form the vertices of a regular icosahedron.

See https://socratic.org/s/aNK5kxwR
cos ((2pi)/5) = 1/2 varphi
See: https://socratic.org/s/aNK5EFJX
Essentially due to its simple properties, it occurs in many contexts.

