Can you help me with this double integral?
#int_0^1int_(3y)^3e^(x^2)dxdy#
1 Answer
Jun 11, 2018
Similar to your previous question, change the order of integration.
Explanation:
We have
Graph those lines:
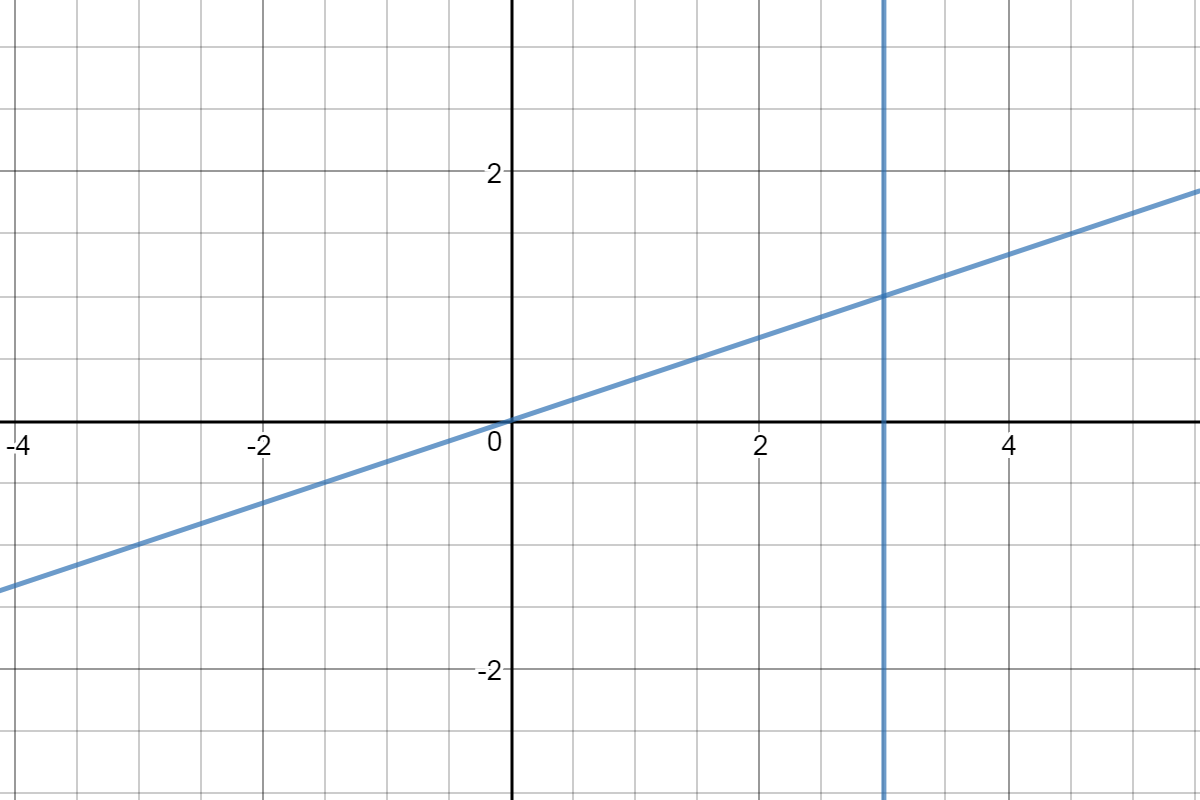
We need
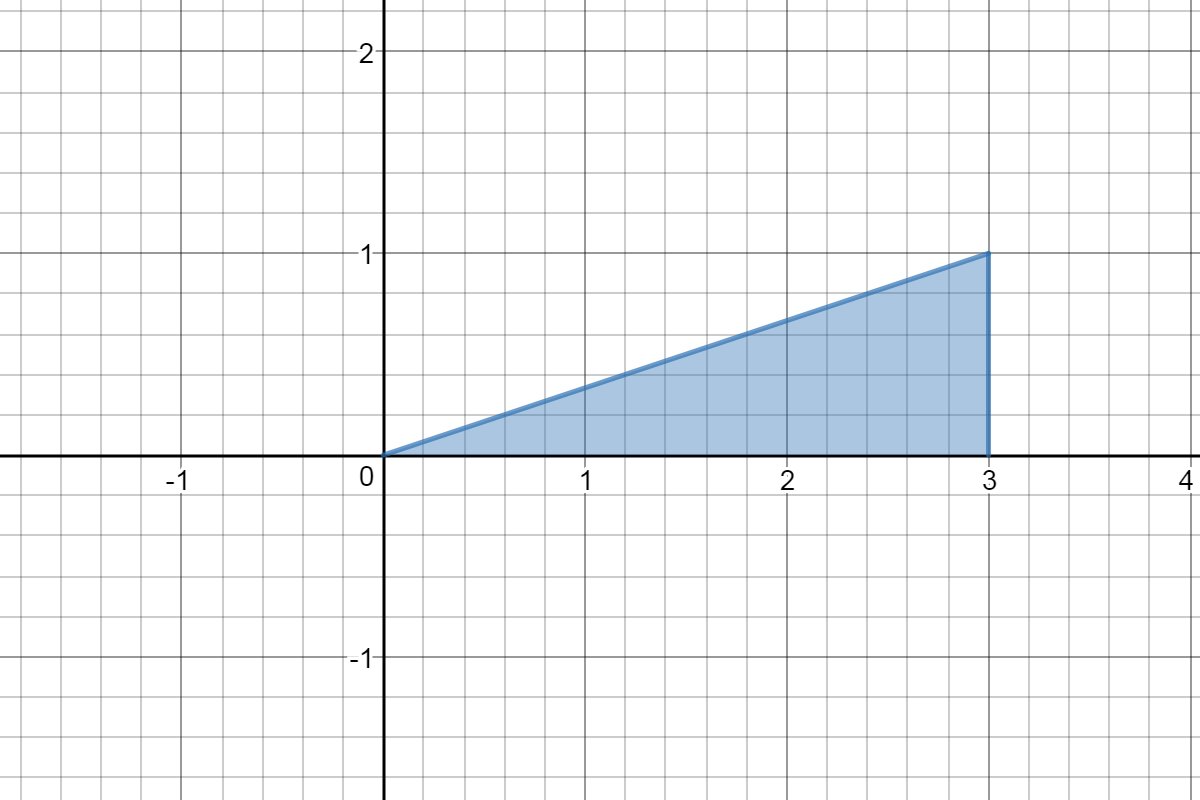
To change the order of integration, we'll need limits of integrating for
So we need to evaluate

