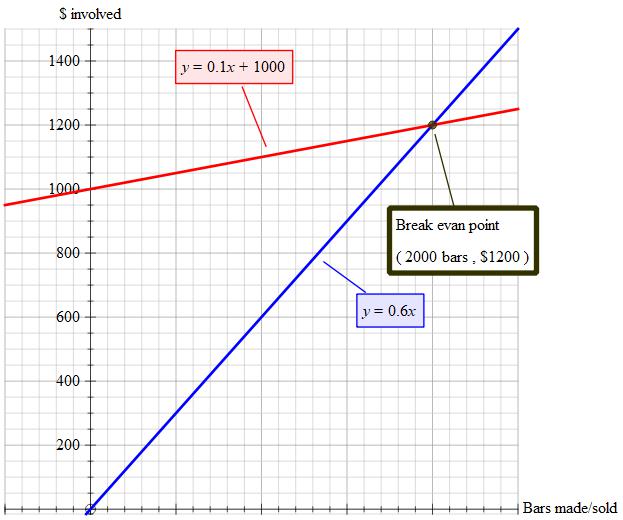
Candy bars are sold in a local store for 60 cents each. The factory has $1000 in fixed costs plus 10 cents of additional expense for each candy bar made. Assuming all candy bars manufactured can be sold, find the break-even point?
2 Answers
Produce of
Explanation:
Break-even point is the number of units
which make zero profit.
Revenue earned ,
additional cost per unit and fixed cost respectively.
So, break-even point is
2000 bars at $1200
Explanation:
Total selling income = manufacturing cost
Before we begin; notice we have a mixture of units. Cents and dollars. Consequently we need to express these using just one unit of measurement. I choose dollars.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let the count of bars be
Total selling income
Production cost
Setting one against the other for break even point.
Dropping the dollar sign as we will just end up with a count (n)