Question

Central limit theorem?

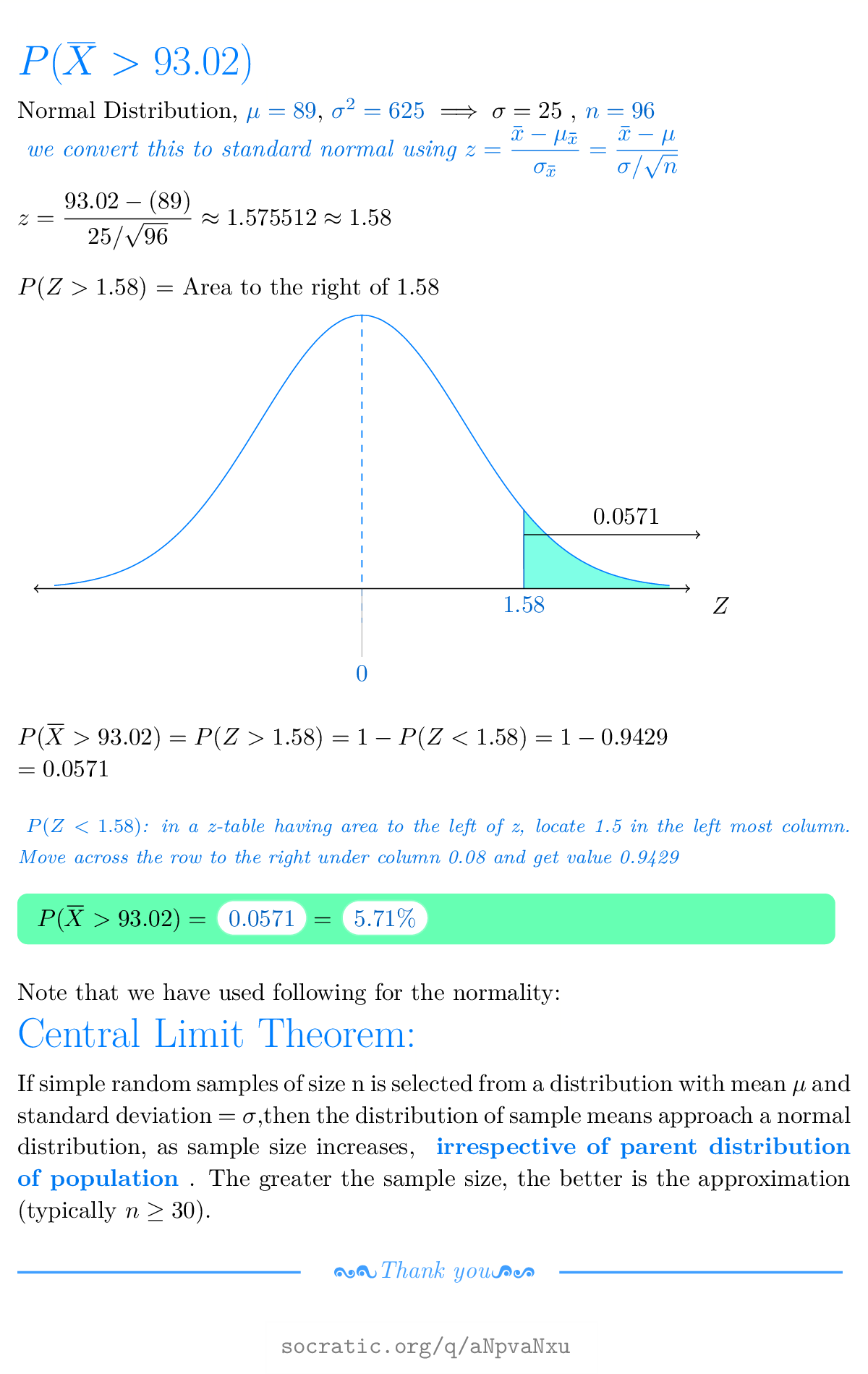
The mean number of words per minute (WPM) read by sixth graders is 89 with a variance of 625.

If 96 sixth graders are randomly selected, what is the probability that the sample mean would be greater than 93.02 WPM? Round your answer to four decimal places.

Thank you

Answer 1

see below

Explanation:

We are not told what the background distribution is. But because the sample size is greater than `30` we can use the central Limit theorem.

it states that for any distribution if the population mean is `mu` and standard deviation is `sigma`. Then if samples of size `n>30` are taken the sampling distribution of the mean is approximately

`barX~N(mu,sigma^2/sqrtn)`

in this case we have

`barX~N(89,625/sqrt96)`

`:.P(barX>93.02)=P(Z>(93.02-89)/(sqrt(625/96)))`

`P(Z>1.5756)`

`=1-P(Z<1.5756)`

using tables

`~~1-0.9429~~0.0571`

Answer 2