Check my work? which statement is true?
2 Answers
The fourth one
Explanation:
If I understood correctly, this is the figure: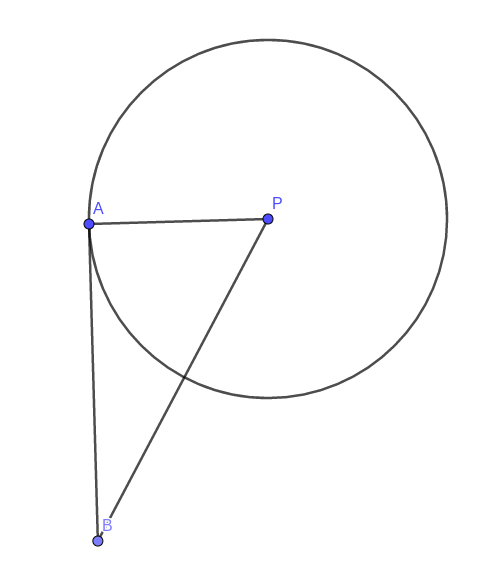
As you can see,
In general, we know that everytime you draw a tangent line to a circle, and the line intersects the circle in a certain point
So, in this case, the line in which
Answer should be 4(
Explanation:
Dear hjjhk,
According to me,correct answer should be 4(
- REASON:
The question states as-
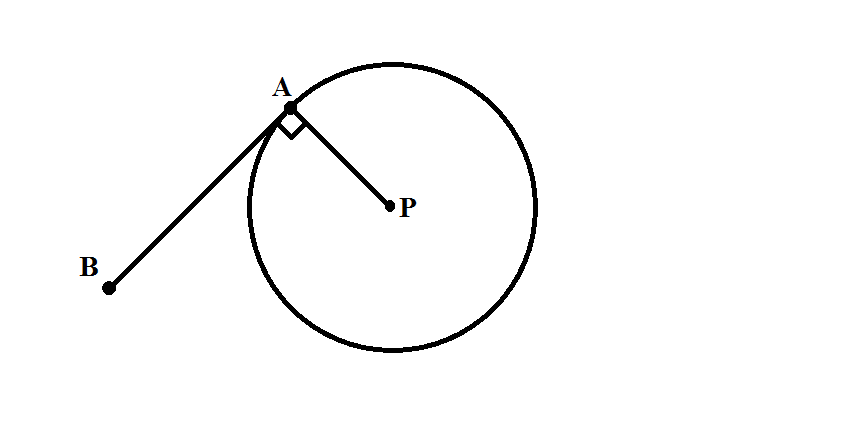
Where,
The a Radius Perpendicular Theorem states, Radius is always perpendicular to the tangent.
-
Option 1:
Option 1 is impossible as it is always right angle. -
Option 2:
Option 2 is not correct in any sense because pointB lies out of the circle as tangent is drawn to the circle. So, radiusPA cannot be equal toPB . -
Option 3:
Option 3 may be correct in limiting case but it is not always correct. -
Option 4:
Option 4 must be correct because Radius is always perpendicular to the tangent.

