Check whether the rectangle of maximum area which can be inscribed in a circle is a square?
1 Answer
Consider a circle of radius
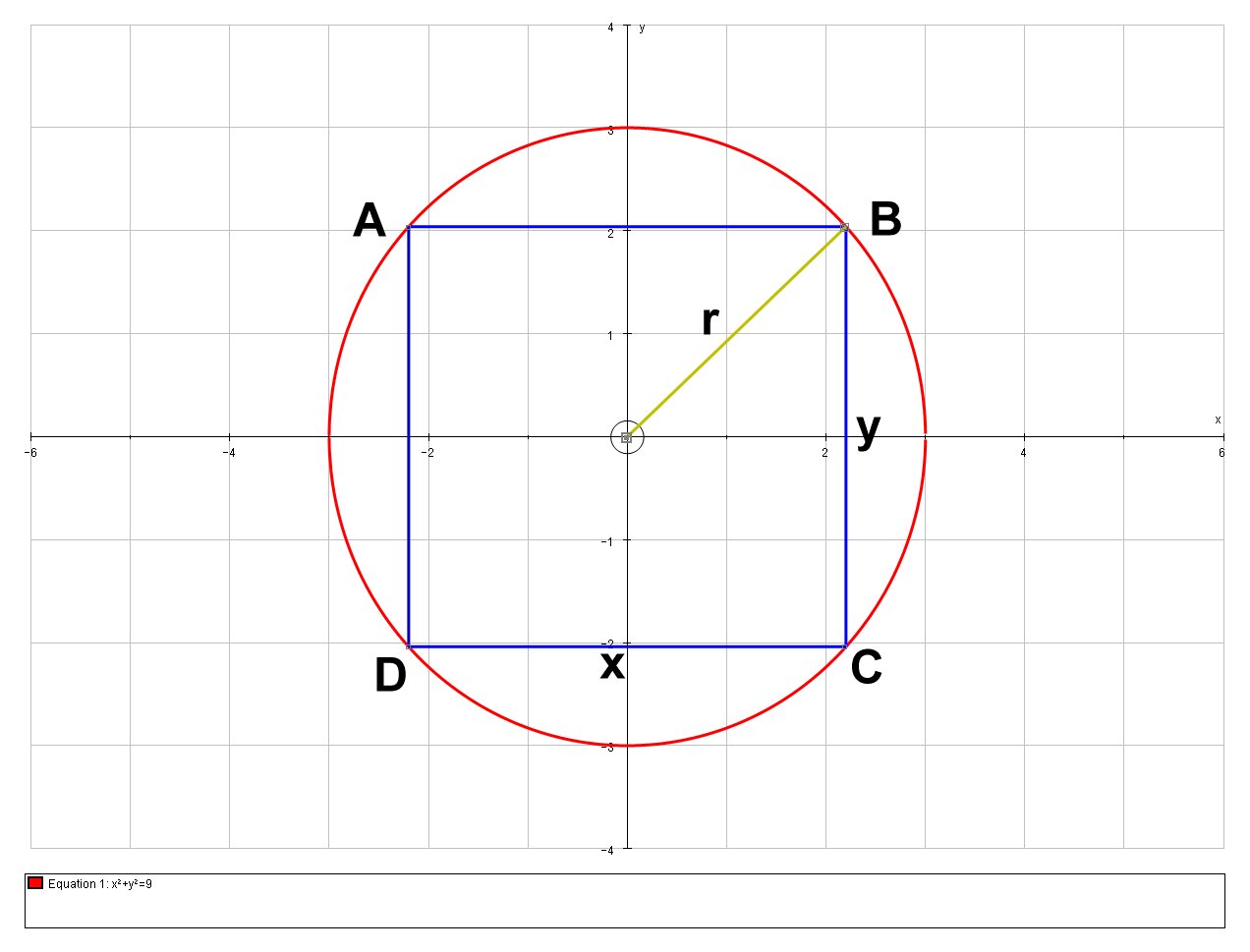
Let
# OA=OB=OC=OD=r#
Let
Let us denote the area of the rectangle
# A = xy # ..... [A]
Also, the
# BD^2 = BC^2 + CD^2 #
# :. (2r)^2 = y^2 + x^2 #
# :. x^2 + y^2 = 4r^2 #
# :. y = sqrt(4r^2 -x^2)# .... [B]
Substitution into [A] gives:
# A = xsqrt(4r^2 -x^2) #
We want to maximise
#(dA)/dx = 0#
Differentiating wrt
# (dA)/dx = (x)(d/dx sqrt(4r^2 -x^2)) + (d/dx x)(sqrt(4r^2 -x^2)) #
# " " = x(1/2 1/sqrt(4r^2 -x^2) * (-2x)) + sqrt(4r^2 -x^2) #
# " " = (4r^2 -x^2-x^2)/(sqrt(4r^2 -x^2)) #
# " " = (4r^2 -2x^2)/(sqrt(4r^2 -x^2)) #
At a maximum or minimum we have
# (dA)/dx = 0 #
# :. (4r^2 -2x^2)/(sqrt(4r^2 -x^2)) = 0 #
# :. 4r^2 -2x^2 = 0 #
# :. x^2 = 2r^2 #
# :. x = sqrt(2)r #
Using [B] this gives:
# y = sqrt(4r^2 -2r^2)#
# \ \ = sqrt(2r^2)#
# \ \ = sqrt(2)r#
Thus we require
NB: We should validate that this value of

