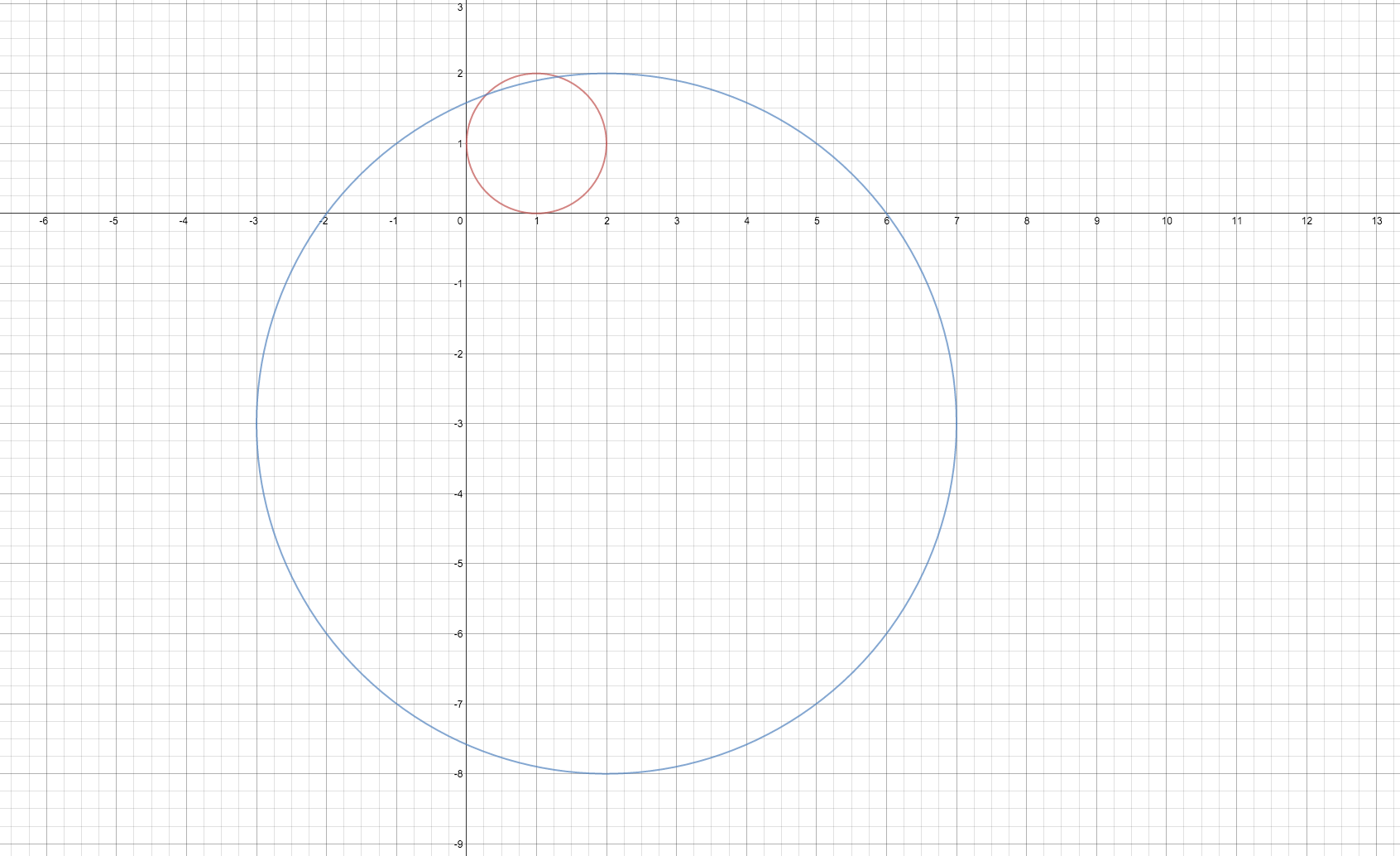
Circle A has a center at #(1 ,1 )# and a radius of #1 #. Circle B has a center at #(2 ,-3 )# and a radius of #5 #. Do the circles overlap? If not, what is the smallest distance between them?
1 Answer
points of intersection:
Explanation:
Recall that the general equation of a circle is:
#(x-h)^2+(y-k)^2=r^2#
where:
Circle A
#(x-1)^2+(y-1)^2=1^2# Circle B
#(x-2)^2+(y+3)^2=5^2#
Circle A
#(x-1)^2+(y-1)^2=1^2#
#(x-1)(x-1)+(y-1)(y-1)=1#
#(x^2-2x+1)+(y^2-2y+1)=1# Equation
#1# :#color(orange)(x^2+y^2-2x-2y+1=0)# Circle B
#(x-2)^2+(y+3)^2=5^2#
#(x-2)(x-2)+(y+3)(y+3)=25#
#(x^2-4x+4)+(y^2+6y+9)=25# Equation
#2# :#color(blue)(x^2+y^2-4x+6y-12=0)#
#color(orange)(x^2+y^2-2x-2y+1)=color(blue)(x^2+y^2-4x+6y-12)#
#color(red)cancelcolor(orange)(x^2)color(red)cancelcolor(orange)(+y^2)color(orange)(-2x-2y+1)=color(red)cancelcolor(blue)(x^2)color(red)cancelcolor(blue)(+y^2)color(blue)(-4x+6y-12)#
#color(orange)(-2x-2y+1)=color(blue)(-4x+6y-12)#
#color(orange)(-2y)# #color(blue)(-6y)=color(blue)(-4x)# #color(orange)(+2x)# #color(blue)(-12)# #color(orange)(-1)#
#-8y=-2x-13#
#(-8y)/(-8)=(-2x)/(-8)-13/(-8)#
#color(purple)(y=1/4x+13/8)#
#color(orange)(x^2+color(purple)y^2-2x-2color(purple)y+1=0)#
#x^2+color(purple)((1/4x+13/8))^2-2x-2color(purple)((1/4x+13/8))+1=0#
#x^2+color(purple)((1/4x+13/8)(1/4x+13/8))-2x-2color(purple)((1/4x+13/8))+1=0#
#x^2+(1/16x^2+13/16x+169/64)-2x-color(red)cancelcolor(black)2^1color(purple)((1/color(red)cancelcolor(purple)4^2x+13/color(red)cancelcolor(purple)8^4))+1=0#
#17/16x^2+13/16x+169/64-2x-1/2x-13/4+1=0#
#17/16x^2-27/16x+25/64=0#
#x=(-b+-sqrt(b^2-4ac))/(2a)#
#x=(-(color(gold)(-27/16))+-sqrt((color(gold)(-27/16))^2-4(color(turquoise)(17/16))(color(brown)(25/64))))/(2(color(turquoise)(17/16)))#
#x=(27/16+-sqrt(729/256-425/256))/(17/8)#
#x=(27/16+-sqrt(304/256))/(17/8)#
#x=(27/16+-sqrt(19)/4)/(17/8)#
#x=(27/16+-(4sqrt(19))/16)xx8/17#
#x=((27+-4sqrt(19))/color(red)cancelcolor(black)16^2)xxcolor(red)cancelcolor(black)8^1/17#
#color(green)(|bar(ul(color(white)(a/a)x=(27+-4sqrt(19))/34color(white)(a/a)|)))#
Intersection 1
#color(purple)(y=1/4x+13/8)#
#y=1/4((27+4sqrt(19))/34)+13/8#
#y=(27+4sqrt(19))/136+13/8#
#y=(27+4sqrt(19))/136+(17(13))/136#
#y=(27+4sqrt(19))/136+221/136#
#y=(248+4sqrt(19))/136#
#y=(4(62+sqrt(19)))/(4(34))#
#y=(color(red)cancelcolor(black)4(62+sqrt(19)))/(color(red)cancelcolor(black)4(34))#
#color(green)(|bar(ul(color(white)(a/a)y=(62+sqrt(19))/34color(white)(a/a)|)))# Intersection 2
#color(purple)(y=1/4x+13/8)#
#y=1/4((27-4sqrt(19))/34)+13/8#
#y=(27-4sqrt(19))/136+13/8#
#y=(27-4sqrt(19))/136+(17(13))/136#
#y=(27-4sqrt(19))/136+221/136#
#y=(248-4sqrt(19))/136#
#y=(4(62-sqrt(19)))/(4(34))#
#y=(color(red)cancelcolor(black)4(62-sqrt(19)))/(color(red)cancelcolor(black)4(34))#
#color(green)(|bar(ul(color(white)(a/a)y=(62-sqrt(19))/34color(white)(a/a)|)))#
If you graphed the two circles, it would look like:
Zoomed in, you can get a sense as to where the intersections are: