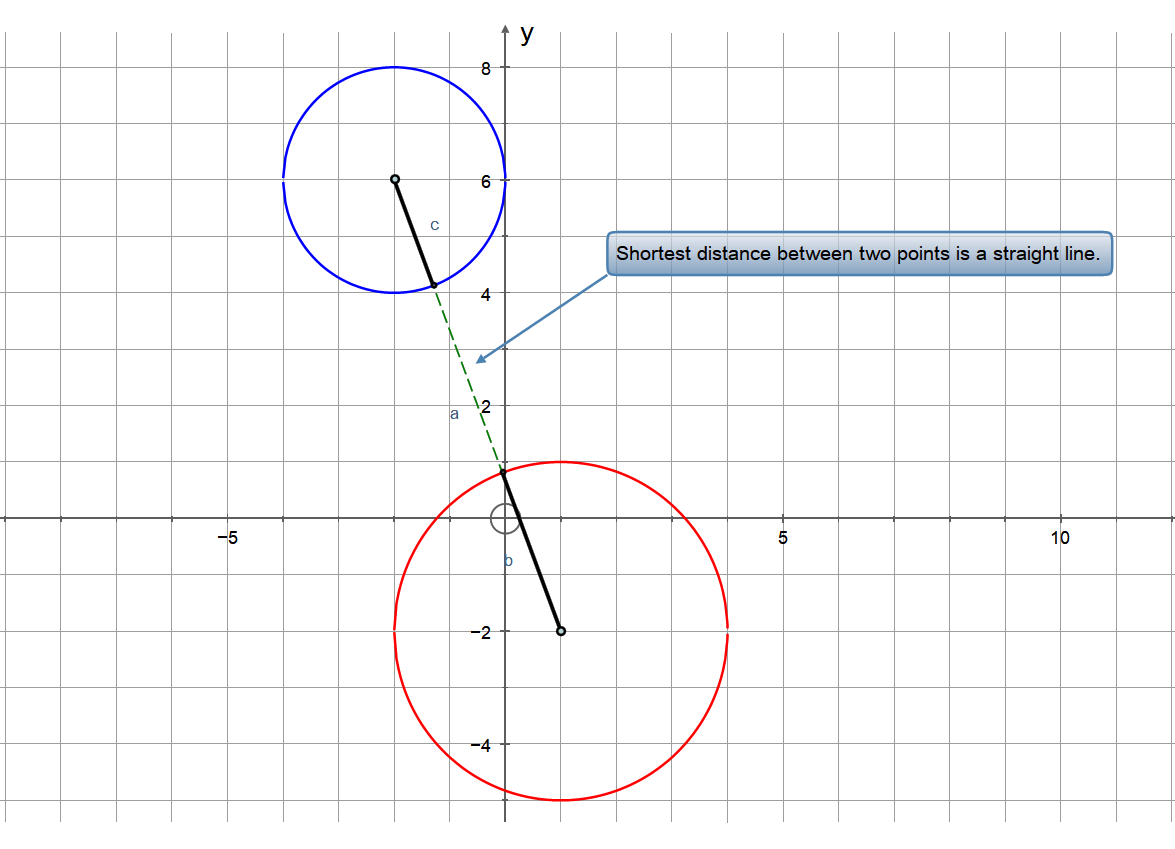
Circle A has a center at #(1 ,-2 )# and a radius of #3 #. Circle B has a center at #(-2 ,6 )# and a radius of #2 #. Do the circles overlap? If not, what is the smallest distance between them?

Question

1398 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-04-24T20:38:26

#color(blue)(sqrt(73)-5)#

Let #d= "the distance between centres"#

Let #s= "the sum of the radii"#

Then if:

#d=s# the circles touch at one point.

#d>s# the circles do not touch.

#d < s# the circles intersect at two points.

We find the distance between centres using the distance formula:

#d=sqrt((x_2-x_1)^2+(y_2-y_1)^2)#

We have:

#A=(1,-2)#

#B=(-2,6)#

#d=sqrt((1-(-2))^2+((-2)-6)^2)=sqrt(73)#

Radius of #A=3#

Radius of #B=2#

Sum of radii:

#3+2=5#

#:.#

#sqrt(73)>5#

The circles do not touch.

The shortest distance between the circles is:

#d-s#

#sqrt(73)-5#

See diagram:

enter image source here