Circle A has a center at #(1 ,4 )# and an area of #28 pi#. Circle B has a center at #(7 ,9 )# and an area of #8 pi#. Do the circles overlap? If not, what is the shortest distance between them?

Question

1343 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-02-10T10:00:54

Since sum of radii greater than the distance between the centers, Circles Overlap

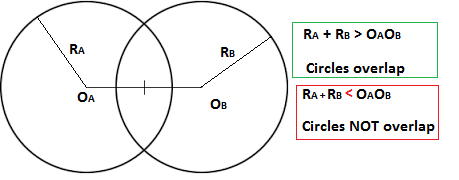
enter image source here

Given : Circle A - #O_A 91,4), A_A = 28pi#, Radius #R_A#

Circle B - #O_B (1,4), A_B = 28pi#, Radius #R_B#

#R_A = sqrt(A_A / pi) = sqrt((28pi)/pi) ~~ 5.29#

#R_B= sqrt(A_B / pi) = sqrt((8pi)/pi) ~~ 2.83#

Sum of Radii #R_A + R_B = 5.29 + 2.83 = color(red)(8.12#

Using distance formula,

#vec(O_AO_B) = sqrt((7-1)^2 + (9-4)^2) ~~ color(red)(7.81#

Since sum of radii greater than the distance between the centers, Circles Overlap