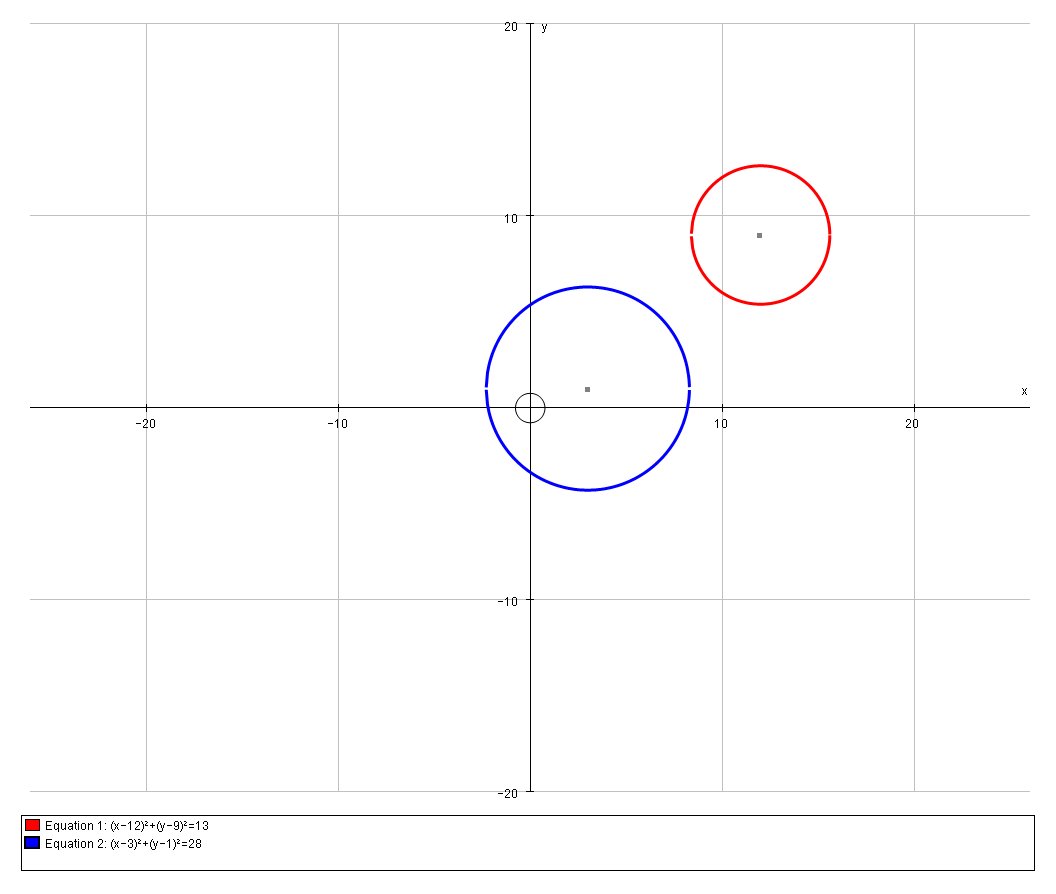
Circle A has a center at #(12 ,9 )# and an area of #13 pi#. Circle B has a center at #(3 ,1 )# and an area of #28 pi#. Do the circles overlap?

Question

942 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-07-03T09:55:19

No

Circle #A# has a centre #(12,9)# and an area of #13 pi#. Thus:

# pi(r_A)^2 = 13pi => r_A=sqrt(13) ~~ 3.61 #

Circle #B# has a centre #(3,1 )# and an area of #28 pi#. Thus:

# pi(r_B)^2 = 28pi => r_B=sqrt(28) ~~ 5.29 #

We can find the distance #AB# using Pythagoras:

# AB^2 = (12-3)^2 + (9-1)^2 #
# " " = 9^2 + 8^2 #
# " " = 81+64 #
# " " = 145 => AB = sqrt(145) ~~ 12.04#

And as #AB gt r_A _ r_B => # The circles do not overlap.

enter image source here