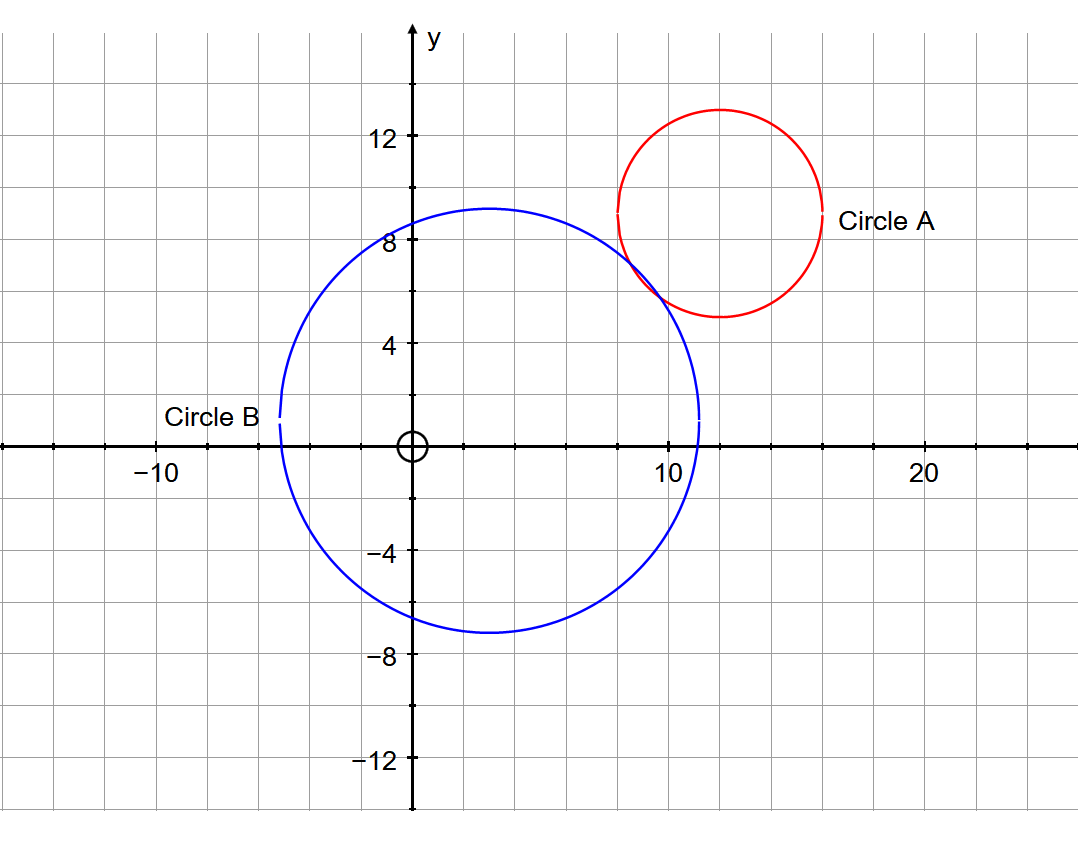
Circle A has a center at #(12 ,9 )# and an area of #16 pi#. Circle B has a center at #(3 ,1 )# and an area of #67 pi#. Do the circles overlap?

Question

1327 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-04-27T08:10:06

Yes.

First we need to find the radii of the circles. We can do this using the formula for area:

#"Area=pir^2#

Circle A

#pir^2=16pi#

#r^2=16=>r=sqrt(16)=4#

Circle B

#pir^2=67pi#

#r^2=67=>r=sqrt(67)#

We now find the distance between the centres. We can use the distance formula for this:

#d=sqrt((x_2-x_1)^2+(y_2-y_1)^2)#

Coordinates #(12,9) , (3,1)#

#d=sqrt((12-3)^2+(9-1)^2)=sqrt(145)#

Let # \ \ \ \d="distance between centres"#

and # \ \ \ s="sum of radii"#

If:

#s=d \ \ \ \ \# circles touch at one point.

#s > d \ \ \ \ \# circles intersect at two points.

#s < d \ \ \ \ \ \#circles do not touch.

Sum of radii:

#4+sqrt(67)#

#4+sqrt(67)>sqrt(145)#

This shows the circles intersect at two points.

enter image source here