Question

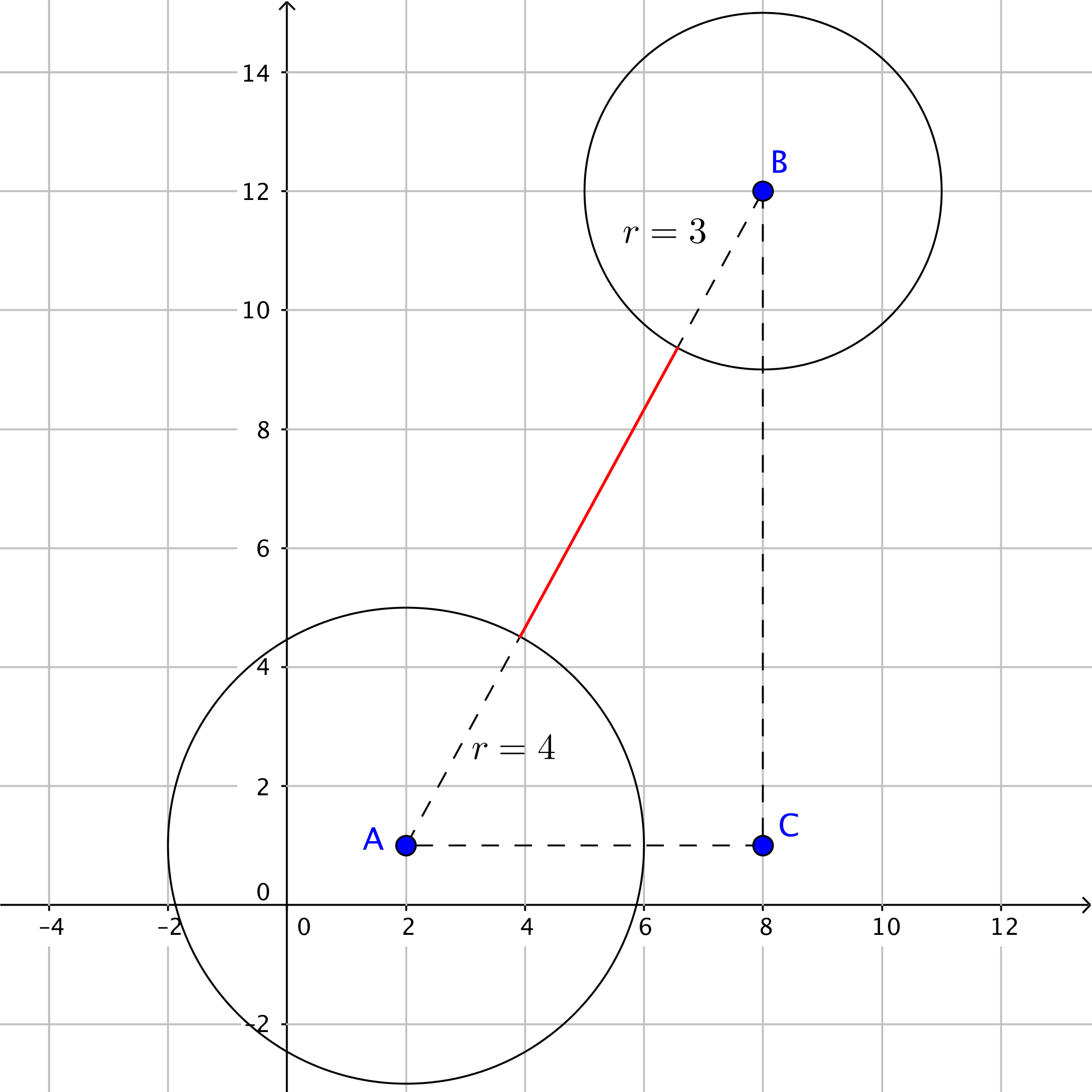
Circle A has a center at `(2 ,1 )` and an area of `16 pi`. Circle B has a center at `(8 ,12 )` and an area of `9 pi`. Do the circles overlap? If not, what is the shortest distance between them?

Answer 1

They do not overlap and the shortest distance is 5.53.

Explanation:

First we calculate the radius of the circles.
We know that the area is given by

Area`=pir^2`
Then the radius of the circle A is `r_A=4` and the radius of the circle B is `r_B=3`.
Now we can plot them as in the picture

We now calculate the distance between the centers.

`AB=sqrt(AC^2+CB^2)=sqrt((x_B-x_A)^2+(y_B-y_A)^2)`
`=sqrt((8-2)^2+(12-1)^2)=sqrt(36+121)\approx12.53`.

This is the distance between the two centers that is bigger than the sum of the two radius given by `r_A+r_B=3+4=7`. So the two circles do not overlap (as we can see from the picture).
The minimum distance between the circles is given by the distance between the two centers minus the two radius:

`d=12.53-3-4=5.53`.