Circle A has a center at #(2 ,2 )# and a radius of #2 #. Circle B has a center at #(5 ,9 )# and a radius of #3 #. Do the circles overlap? If not what is the smallest distance between them?

Question

1959 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-04-13T05:23:58

#color(crimson)("Since " bar(AB) > r + r', " two circles do not overlap"#

#color(blue)("Smallest distance between the circles " = bar(AB) - r - r' #

#color(brown)(=> 7.62 - 2 - 3 = 2.62#

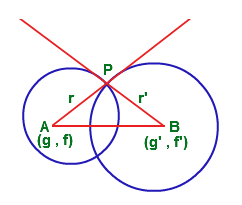
From the figure above,

#color(purple)("The two circles A & B overlap each other if "#

#color(purple)(bar(AB) < r + r'#

#color(purple)("Touch each other if " bar(AB) = r + r'#

#color(purple)("Do not intersect if " bar(AB) > r + r'#

#"Given : Circle A " (g,f) = (2,2), r = 2#

#"Given : Circle B " (g',f') = (5,9), r' = 3#

#bar(AB) = sqrt((g-g')^2 + (f - f')^2)#

#bar (AB) = sqrt ((2-5)^2 + (2-9)^2) ~~ 7.62#

#r + r' = 2 + 3 = 5#

#color(crimson)("Since " bar(AB) > r + r', " two circles do not overlap"#

#color(blue)("Smallest distance between the circles " = bar(AB) - r - r' #

#color(brown)(=> 7.62 - 2 - 3 = 2.62#