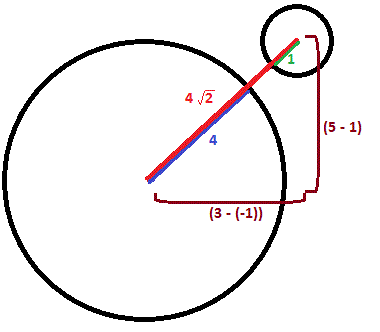Circle A has a center at #(3 ,5 )# and a radius of #1 #. Circle B has a center at #(-1 ,1 )# and a radius of #4 #. Do the circles overlap? If not, what is the smallest distance between them?
1 Answer
Feb 2, 2016
The circles do not overlap.
The minimum distance between them is
Explanation:
The distance between the centers of the two circles is
Consider a line segment joining the two centers.
The distance from A's center to A's circumference is
The distance from B's center to B's circumference is
The sum of the radial distances is
by