Question

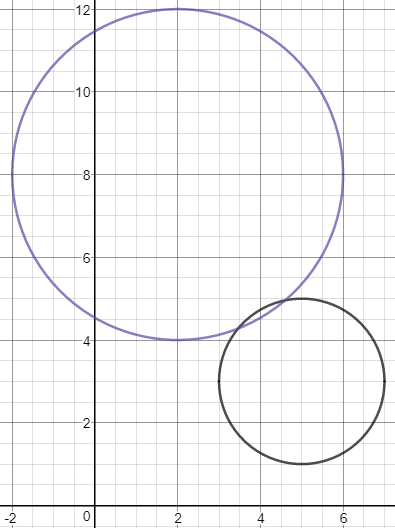
Circle A has a center at `(5 ,3 )` and an area of `4 pi`. Circle B has a center at `(2 ,8 )` and an area of `16 pi`. Do the circles overlap? If not, what is the shortest distance between them?

Answer 1

Yes, they overlap.

Explanation:

Generally, we know that for a circle with radius `r`,
`A=pir^2`

In the case of these circles, we are given the area which we can solve for. Let's start with circle `A`:

We know the area is `4pi`, so we'll plug that in and solve for radius:

`4pi=pir^2`
`4=r^2`
`sqrt(4)=r`
`2=r_A`

We'll do the same for circle `B`:

`16pi=pir^2`
`16=r^2`
`sqrt(16)=r`
`4=r_B`

We'll keep this in mind until a bit later.

We need to take the centers of the circles and see how far apart they are. If this distance is larger than the sum of the radii, then they do not intersect. If this distance is smaller than the sum, then they intersect twice. If this distance is equal to the sum, they intersect exactly once.

`r_A+r_B=r_"sum"`
`2+4=6`
We know the two radii are `2` and `4`, so their sum is obviously `6`.

We also know their centers, which are `(5,3)` and `(2,8)`. Using the Pythagorean Theorem, we can find the distance between these two points:

`a^2+b^2=c^2`
`(5-2)^2+(3-8)^2=c^2`
`3^2+(-5)^2=c^2`
`9+25=c^2`
`34=c^2`
`sqrt34=c`
`2.45~~c`

From this, we can tell that they do intersect, because their combined radii are larger than the distance between the two points.

If they didn't overlap, the closest point between them would be found like this:

You would find the distance between the two centers and the subtract the sum of the radii.

For example, if the two circles were `10` units apart, and one had a radius of `3` and the other had a radius of `2`, you would subtract `3` and `2` from `10` to get `5`. `5` would be the distance between the two closest points.

You can also always graph it: