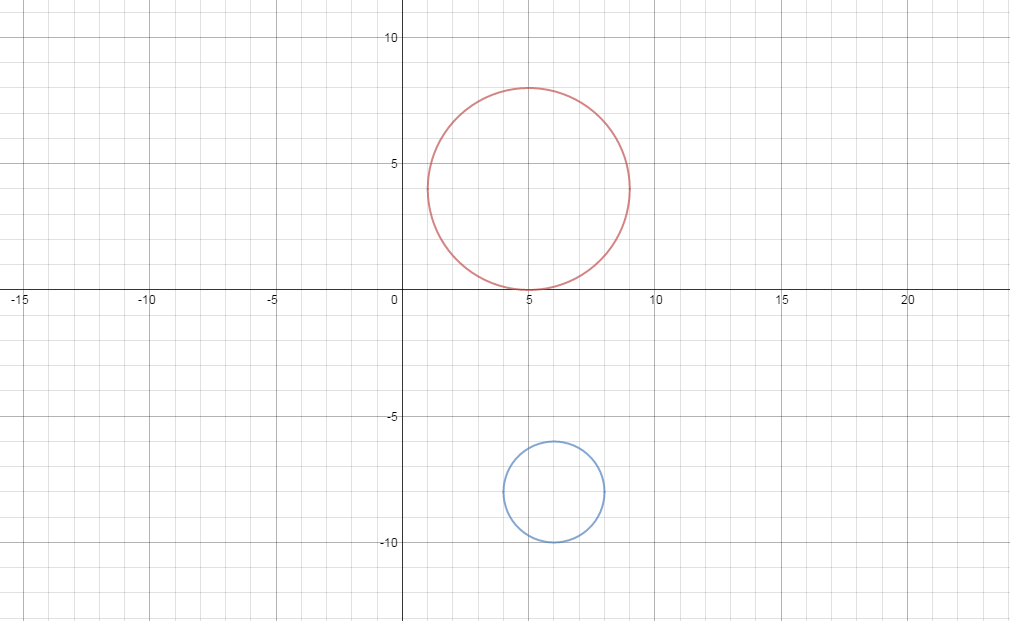
Circle A has a center at (5 ,4 ) and a radius of 4 . Circle B has a center at (6 ,-8 ) and a radius of 2 . Do the circles overlap? If not, what is the smallest distance between them?
1 Answer
Mar 10, 2016
The circles do not overlap.
Smallest distance
Explanation:
From the given data:
Circle A has a center at (5,4) and a radius of 4. Circle B has a center at (6,−8) and a radius of 2. Do the circles overlap? If not, what is the smallest distance between them?
Compute the sum of the radius:
Sum
Compute the distance from center of circle A to center of circle B:
Smallest distance
 desmos.com
desmos.com
God bless....I hope the explanation is useful..
