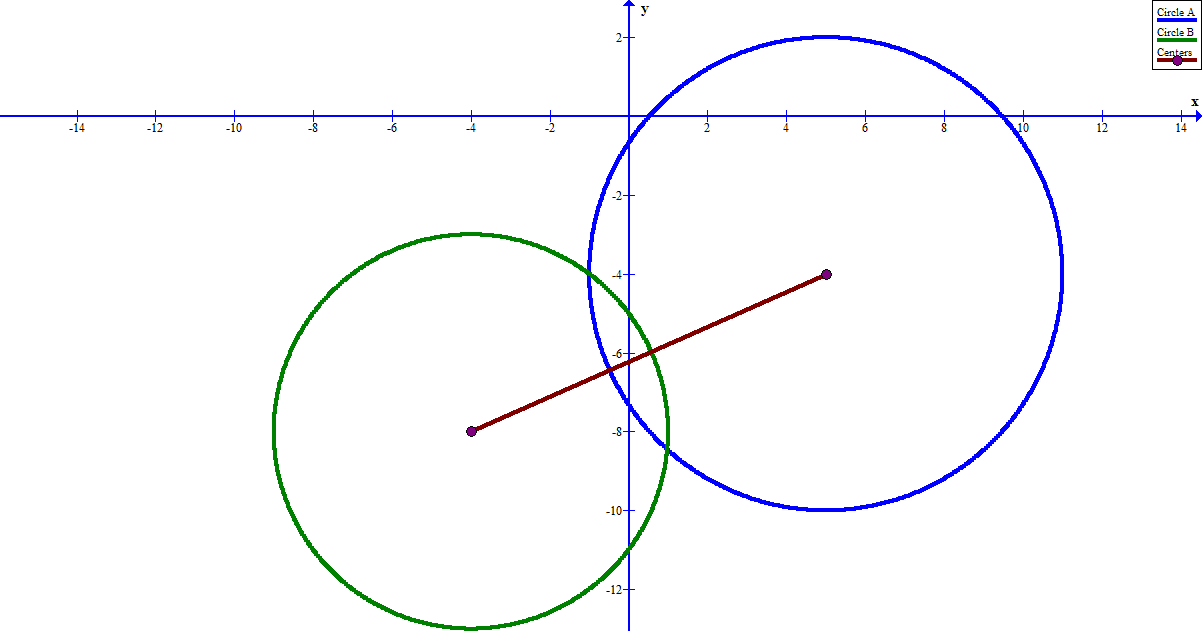Circle A has a center at #(5 ,-4 )# and a radius of #6 #. Circle B has a center at #(-4 ,-8 )# and a radius of #5 #. Do the circles overlap? If not, what is the smallest distance between them?
1 Answer
The circles overlap.
Explanation:
The distance between the center of A at
and the center of B at
is
Circle A with a radius of
covers
and
Circle B with a radius of
covers
Between the two circles,
they cover
Since the distance between them is only (approx.)
the circles must overlap ( by approx.
As verification, here is what the circles look like: