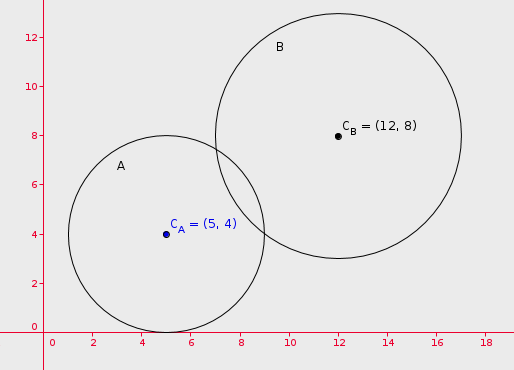
Circle A has a center at (5 ,4 ) and an area of 16 pi. Circle B has a center at (12 ,8 ) and an area of 25 pi. Do the circles overlap? If not, what is the shortest distance between them?
1 Answer
Oct 14, 2017
The given circles intersect
Explanation:
Since the area of a circle is
we get
then
and
then
The distance between the centers is:
that's less than the sum of the radiuses
We conclude that the circles intersect: