#"Strategy:"#
#"1-Find radius of Circle A":color(red)(r_A)#
#"2-Find radius of Circle B":color(red)(r_B)#
#"3-Find distance from Center of Circle A to Center of Circle B":color(red)(d) #
#4-"Compare "color(red)(d)" and "color(red)( r_A+r_B)"#
#"1)........................................................."#
#Area_A=pi*r_A^2" , "78 pi=pi*r_A^2" , "78cancel( pi)=cancel(pi)*r_A^2#
#r_A^2=78" , "r_A=sqrt(78)" , "r_A=8.83" unit"#
#"2).........................................................."#
#Area_B=pi*r_B^2" , "54pi=pi*r_B^2" , "54cancel(pi)=cancel(pi)*r_B^2#
#r_B^2=54" , "r_B=sqrt(54)" , "r_B=7.35" units"#
#"3)..........................................................."#
#d=sqrt((9-7)^2+(2-5)^2)#
#d=sqrt(2^2+(-3)^2)#
#d=sqrt(4+9)#
#d=sqrt(13)#
#d=3.61" units"#
#"4)................................................................."#
#"if d>"r_A+r_B" than no overlap"#
#"if d<"r_A+r_B" than overlap"#
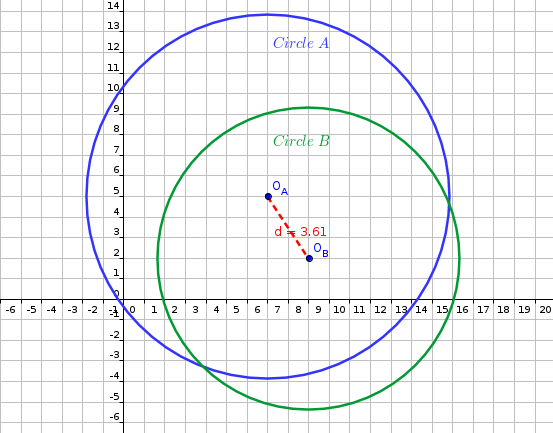
#d=3.61 "units"#
#r_A+r_B=8.83+7.35=16.18#
#"Circles are overlap"#

