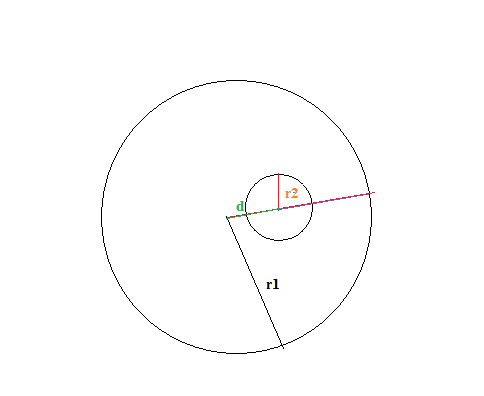
Circle A has a center at #(7 ,5 )# and an area of #92 pi#. Circle B has a center at #(9 ,2 )# and an area of #14 pi#. Do the circles overlap?
1 Answer
Mar 11, 2016
They will overlap,practically smaller one will be inside larger
Explanation:
Given
Area of 1st circle
Hence
Again Area of 2nd circle
Hence
Sum of their radii
Now the distance between their centers
S>d => They will overlap,practically smaller one will be inside larger one because