Circle #O# with diameter #"AB"=6# has point #"C"# on its circumference. If #"AC"⋅"BC"="AB"#, then find the perimeter of #triangle "ABC"#?

Question

This is a tricky question.I tried to my best but could not solve it

Please help, Thank you

1259 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-04-09T14:46:52

perimeter #=6+4sqrt3 ~~12.928#

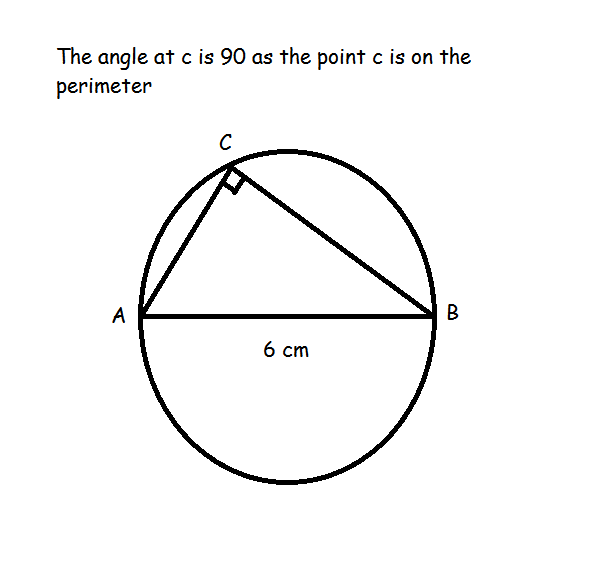
enter image source here

Given that #AB# is the diameter, #=> angleACB=90^@#
#=> AB^2=AC^2+BC^2#
#=> 36 =AC^2+BC^2#

#(AC+BC)^2=AC^2+BC^2+2*AC*BC#
Given #AC*BC=6#
#=> (AC+BC)^2=36+2xx6=48#
#=> AC+BC=sqrt48=4sqrt3#

perimeter of #DeltaABC=AB+AC+BC#
#=6+4sqrt3~~12.928#