Question

Toluene and benzene have vapour pressures at 20 °C of approximately 22 mmHg and 75 mmHg, respectively. Calculate the total pressure of an ideal solution made up of 0.828 mol toluene and 0.172 mol benzene at this temperature?

Answer 1

The total pressure is 31 mmHg.

Explanation:

To solve this problem, we use Raoult's Law:

`color(blue)("The partial vapour pressure of a component in a mixture is equal"`
`color(blue)("to the vapour pressure of the pure component multiplied by its")`
`color(blue)("mole fraction in the mixture.")`

In symbols, the partial vapour pressure `p_text(A)` of component A is given by

`color(blue)(bar(ul(|color(white)(a/a)p_text(A) = chi_text(A)p_text(A)^@color(white)(a/a)|)))" "`

where

`chi_text(A) =` the mole fraction of A
`P_text(A)^@ =` the vapour pressure of pure A

If we have two volatile components A and B, the total pressure `p_text(tot)` over the solution is

`p_text(tot) = chi_text(A)p_text(A)^@ + chi_text(B)p_text(B)^@`

Step 1. Calculate the mole fractions of `bb"A"` and `bb"B"`

Let A = toluene and B = benzene. Then

`chi_text(A) = n_text(A)/(n_text(A) + n_text(B)) = 0.828/(0.828 + 0.172) = 0.828/1.000 = 0.828`

`chi_text(B) = n_text(B)/(n_text(A) + n_text(B)) = 0.172/1.000 = 0.172`

Step 2. Calculate the total pressure

`p_text(tot) = "0.828 × 22 mmHg + 0.172 × 75 mmH"`
`"= 18.2 mmHg + 12.9 mmHg = 31 mmHg"`

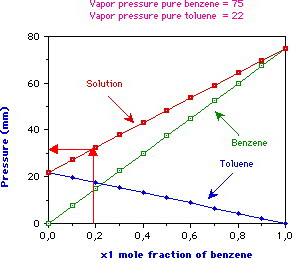
(Adapted from wpage.unina.it)

In the diagram above, you would start at just under 0.2 on the horizontal axis and go up until you hit the line for total pressure.

Then, you would draw a horizontal line to the left until you hit the vertical axis and find a total pressure of about 31 mmHg.