Collision question?
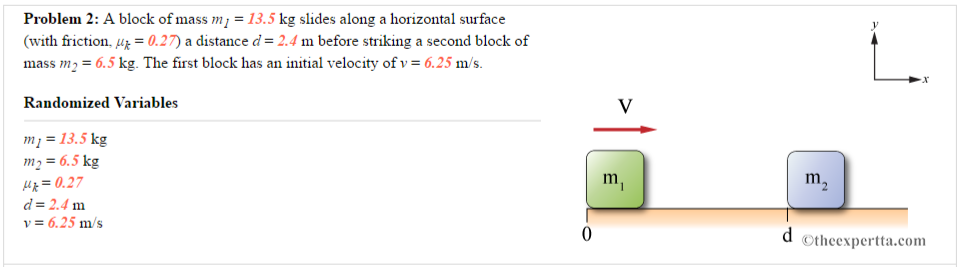
A: Assuming that block one stops after it collides with block two, what is block two's velocity after impact in m/s?
B: How far does block two travel, d2 in meters, before coming to rest after the collision?

A: Assuming that block one stops after it collides with block two, what is block two's velocity after impact in m/s?
B: How far does block two travel, d2 in meters, before coming to rest after the collision?
2 Answers
I get
A.
B.
Results rounded to two decimal places.
Explanation:
A. Initial velocity of block of mass
During sliding movement impeding force of friction
where
Deceleration produced due to this force
using the kinematic expression
Momentum of mass
Given that first block stops after its collision with second block. Due to Law of conservation of momentum, momentum of second block just after the collision
Velocity of second mass
B. Using (1) for Deceleration due friction also for block
See below.
Explanation:
Calling
Before collision
during the collision
after the collision
Solving
for
Putting values

