Complete the table given h(x)=g(f(x)) ?
I'm really confused on how to use composition of functions to complete the table. I was only able to fill in one blank. I would much appreciate some help with steps on how to solve this table.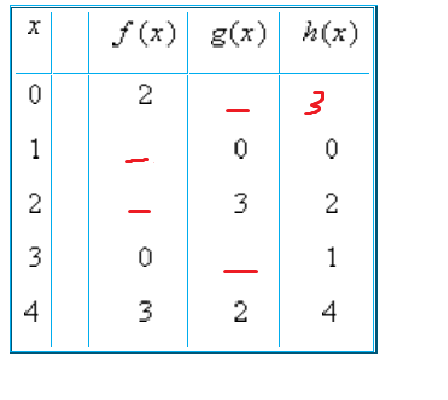
I'm really confused on how to use composition of functions to complete the table. I was only able to fill in one blank. I would much appreciate some help with steps on how to solve this table.
1 Answer
Explanation:
Given (with identification variables added for later reference):
but we are also told that
but we are also told that
From here on, I am not certain that any unique solution is possible
I have assumed that the functions are one-to-one and the range is limited to
If this is the case, the only value remaining for
and
since
and this only leaves
