Consider the following balanced equation. 2N2H4(g)+N2O4(g)→3N2(g)+4H2O(g) ?
Complete the following table, showing the appropriate number of moles of reactants and products. If the number of moles of a reactant is provided, fill in the required amount of the other reactant, as well as the moles of each product formed. If the number of moles of a product is provided, fill in the required amount of each reactant to make that amount of product, as well as the amount of the other product that is made.
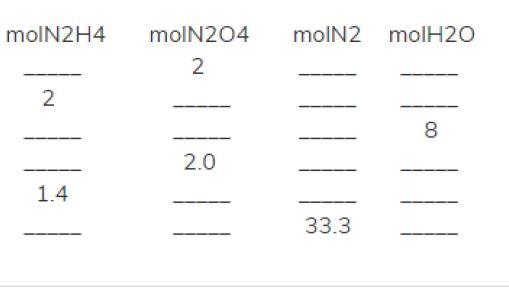
Complete the following table, showing the appropriate number of moles of reactants and products. If the number of moles of a reactant is provided, fill in the required amount of the other reactant, as well as the moles of each product formed. If the number of moles of a product is provided, fill in the required amount of each reactant to make that amount of product, as well as the amount of the other product that is made.

1 Answer
Warning! Long Answer. Here's what I get.
Explanation:
This question involves practice in using molar ratios.
The balanced equation is
#"2N"_2"H"_4 + "N"_2"O"_4 → "3N"_2 +"4H"_2"O"#
Row 1
Do you notice a pattern?
You are using twice as many moles of
The conversion factor is always the molar ratio:
Row 2
You are using the same number of moles of
You can do the calculation using numbers as above, and you will get
Row 3
You are using twice as many moles of
Thus, you will get
Row 4
Row 4 is the same as Row 2, but you are using more precision in your measurements (one more decimal point).
Thus, you get
Row 5
You are using 0.70 times as many moles of
Thus, you will get
Row 6
You are using 11.1 times as many moles of
Thus, you will get

