Consider the following reaction: 2 NO(g) + 2 H2(g) → N2(g) + 2 H2O(g) Use the data below to find the rate law and determine the value of the rate constant? Make sure to report proper units!
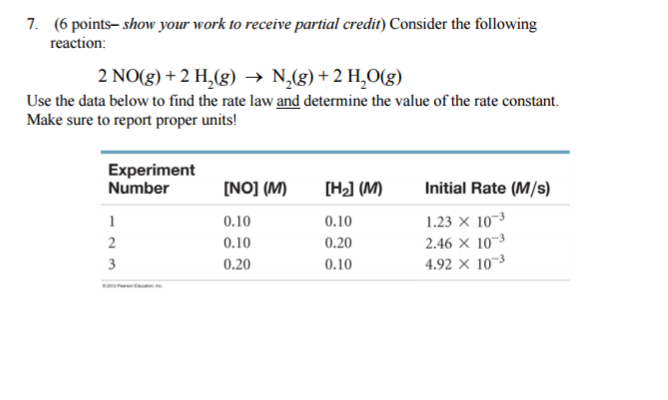
1 Answer
Explanation:
This question is concerned with the method of initial rates which can be used if more than one species is reacting.
In this case, as the reaction proceeds the concentration of both species falls.
We need to keep the concentration of one species constant while varying the concentration of the other.
We do this by measuring the initial rate of reaction because, at this point, the concentration of each species has not fallen.
If you look at experiments 1 and 2 you can see that
How has this affected the initial rate?
It has gone from
This means that there is a linear relationship between the 2 variables so the order with respect to
Now consider experiments 1 and 3. In this case it is
How is the rate affected?
It has gone from
This has been altered by a factor
This indicates that the rate must depend on
Combining both we get the overall rate expression:
To get the value of the rate constant just put in some values from Expt. 1:

