#cos75^@ cos15^@ + sin75^@ sin15^@# ?

Question

4710 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-04-25T00:03:55

#1/2#

Consider a equilateral triangle bisected:

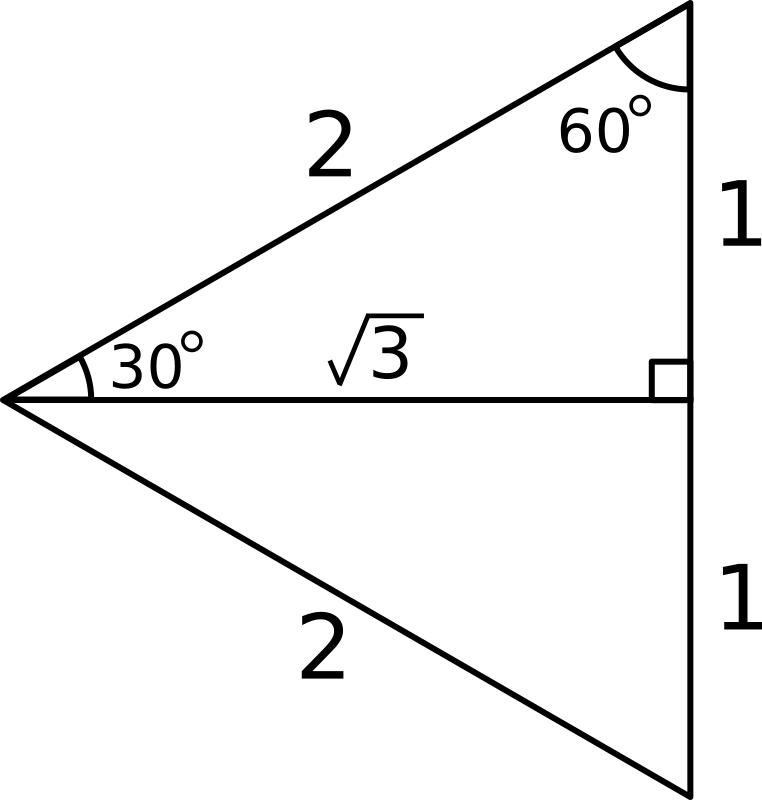
enter image source here

From this we see:

#cos 60^@ = "adjacent"/"hypotenuse" = 1/2#

#sin 30^@ = "opposite"/"hypotenuse" = 1/2#

Method 1

Use:

#cos(alpha-beta) = cos(alpha)cos(beta)-sin(alpha)sin(beta)#

So:

#cos 75^@ cos 15^@ + sin 75^@ sin 15^@ = cos(75^@ - 15^@) = cos 60^@ = 1/2#

Method 2

Use:

#cos(theta) = sin(90^@-theta)#

#sin(theta) = cos(90^@-theta)#

#sin(2theta) = 2 sin theta cos theta#

So:

#cos 75^@ cos 15^@+sin 75^@ sin 15^@ = sin 15^@ cos 15^@ + sin 15^@ cos 15^@ = sin 30^@ = 1/2#