Question

Could anyone please help me with part F?

Answer 1

Please see the explanation below.

Explanation:

The velocity is constant at `t_2=30s`

`(ds)/dt=60kmh^-1`

Therefore,

The acceleration is

`a=(d^2s)/dt^2=d/dt((ds)/dt)=0ms^-2`

Answer 2

The instantaneous acceleration at `t_2= 30` sec. is
`a_2=-10/6 m/s^2 ~~ -1.67 m/s^2`

Explanation:

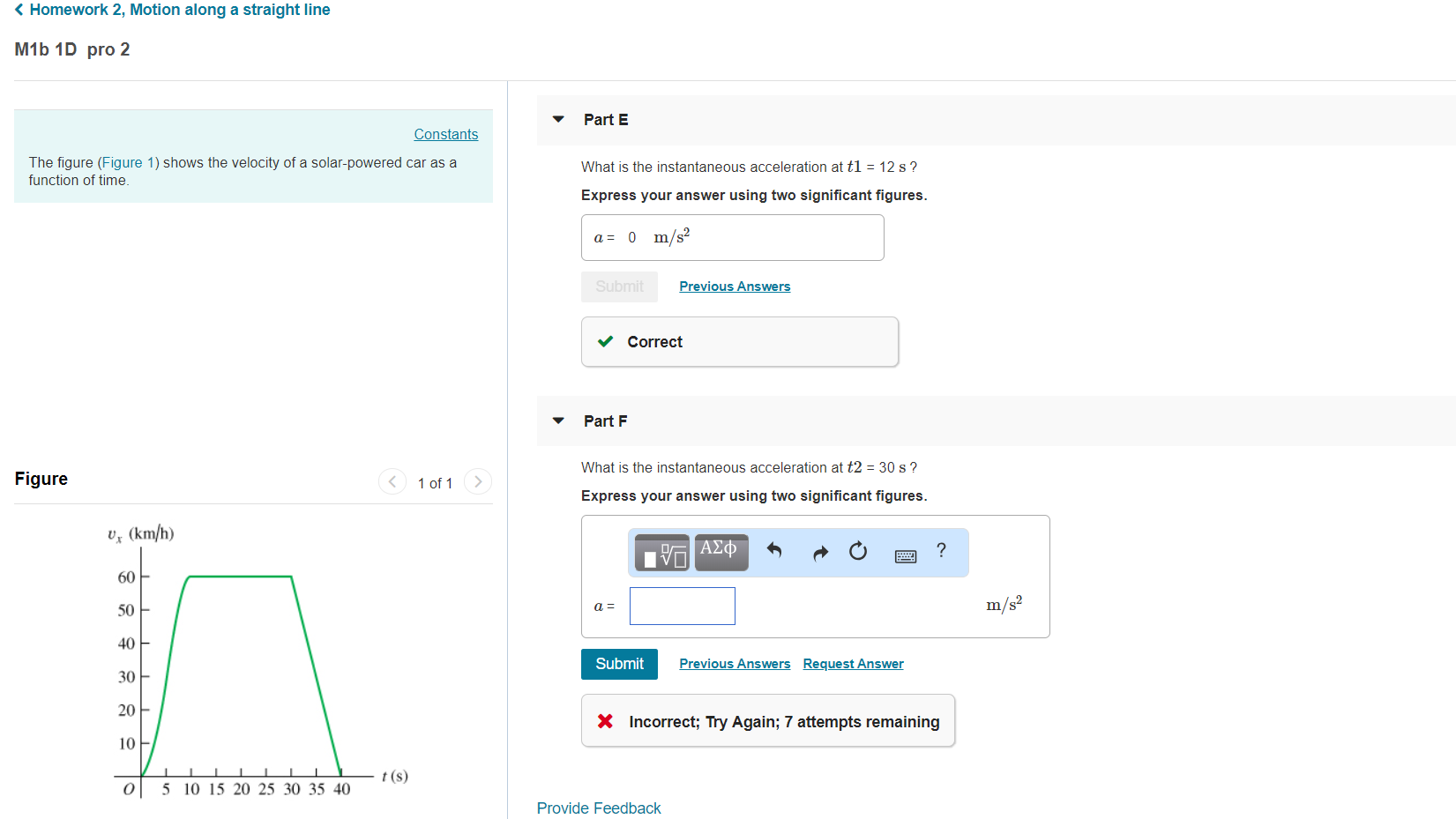
According to the figure we have a constant speed until 30 sec, at which point the movement descelerates, so that the speed changes constantly from 60 km/h to 0 km/h in 10 sec. (from 30 to 40 sec.).

Acceleration is speed change per second, i.e. `(Deltav)/(Delta t)`

We, therefore need to convert the speed from `(km)/h` to `m/s`

`60 (km)/h=60000/3600 m/s=100/6 m/s`

(60 km = 60 000 m, and there are 3600 sec. in 1 hour)

Therefore `a=(Deltav)/(Delta t)`
`=(0-100/6)/10 m/s^2`
`=-10/6 m/s^2=-1.67 m/s^2`

The figure shows that the acceleration is constant from 30 to 40 sec. The instantaneous acceleration at `t_2= 30 s`, therefore, is
`a_2=-10/6 m/s^2 ~~ -1.67 m/s^2`