Could someone please help me with this math question?
Which quadratic equation fits the data in the table?
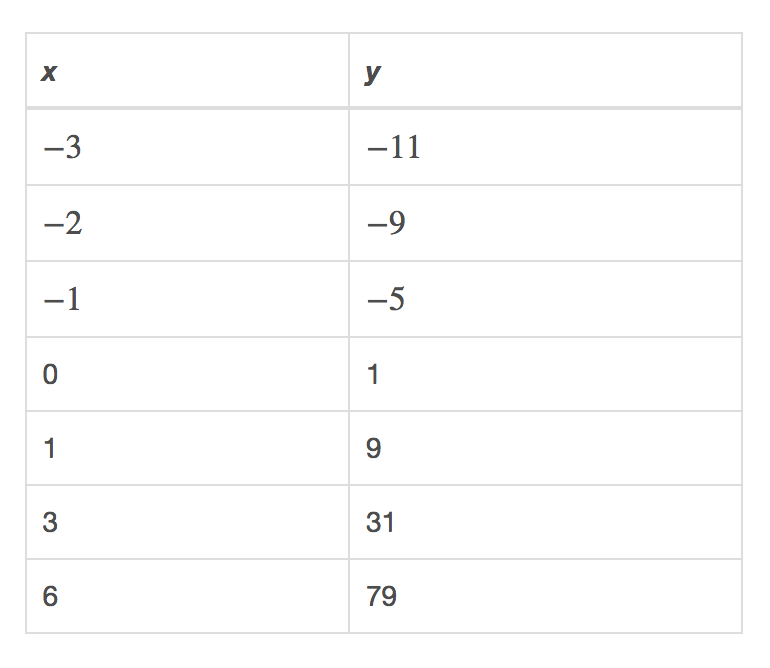
A) y = x² − 7x − 1
B) y = −x² + 7x + 1
C) y = x² −7x + 1
D) y = x² + 7x + 1
Which quadratic equation fits the data in the table?

A) y = x² − 7x − 1
B) y = −x² + 7x + 1
C) y = x² −7x + 1
D) y = x² + 7x + 1
1 Answer
Choice D works.
Explanation:
The table you have with
I looked first at the ordered pair
Any of the others would give you
Another easy point to look at is
For B. we get:
Equation C:
Try D:
So we don't need to try any other coordinate pairs; all of them should work, and these two don't work in equations A,B, or C.
I hope that helps!

