Question

Could someone please tell me how did we get these values for bearings?

Answer 1

`"see explanation"`

Explanation:

`"bearings are given as measures from the "`

`• color(blue)" North line in a clockwise direction"`

`"they are usually expressed as 3 figures"`

`rArr90^@-=090^@`

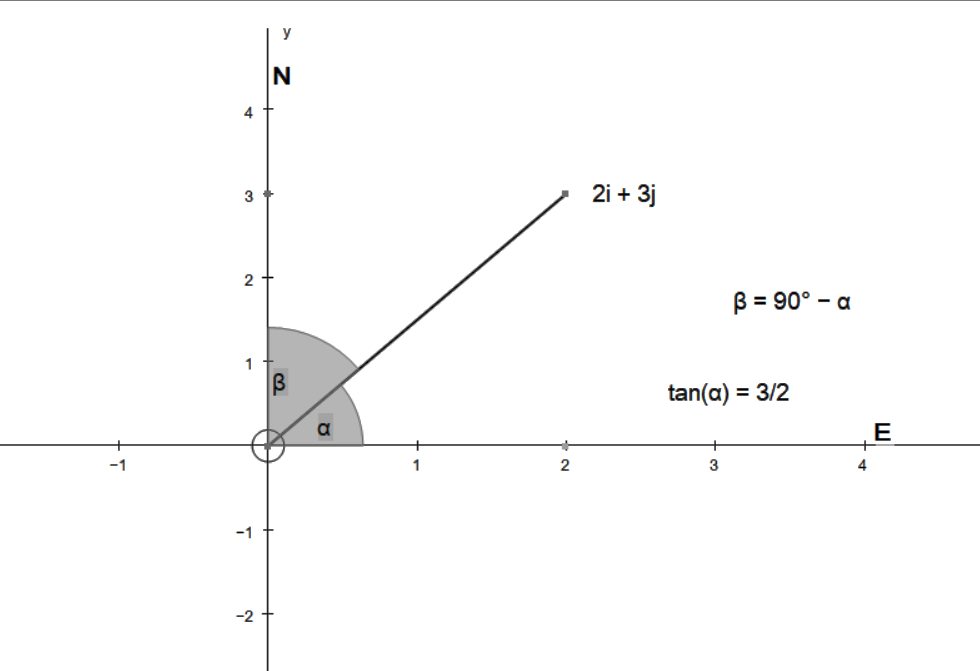
`(a)`

`2i+3j" is positioned in the first quadrant"`

`•color(white)(x)theta=tan^-1(y/x)`

`rArrtheta=tan^-1(3/2)~~56^@larrcolor(blue)"related acute angle"`

`"this angle is measured anticlockwise from the x-axis"`

`rArr"angle from north line "=90-56=34`

`rArr"bearing "=034^@`

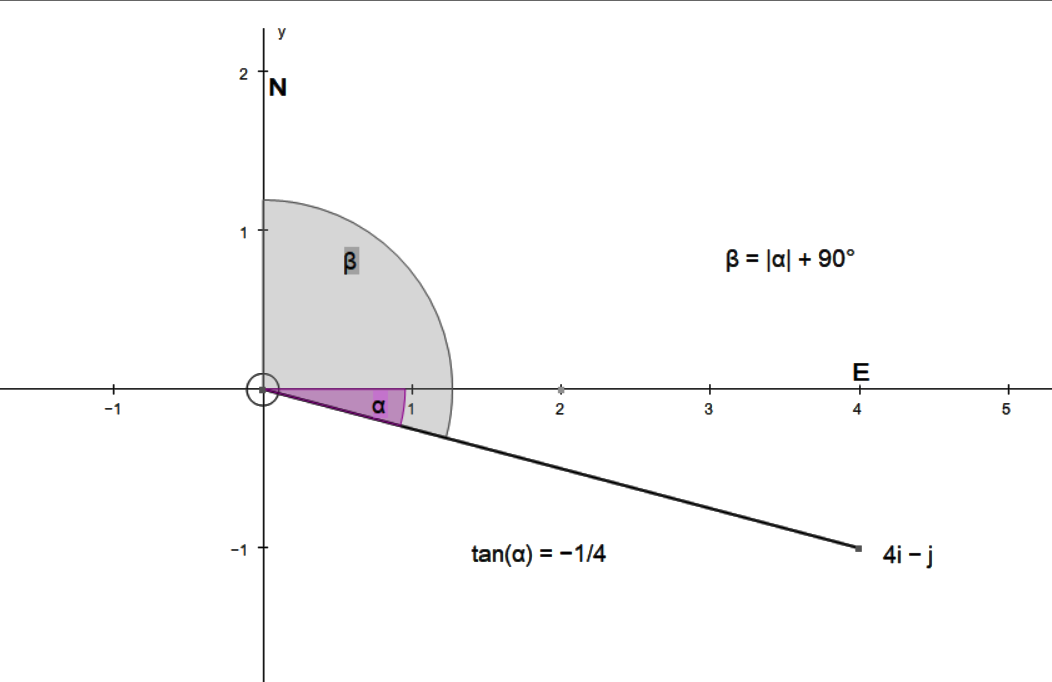
`(b)`

`4i-j" is positioned in the fourth quadrant"`

`theta=tan^-1(1/4)~~14^@larrcolor(blue)"related acute angle"`

`rArr"angle from north line "=90+14=104^@`

`rArr"bearing "=104^@`

`(c)`

`-3i+2j" is positioned in the second quadrant"`

`rArrtan^-1(2/3)~~34^@larrcolor(blue)"related acute angle"`

`rArr"angle from north line "=270+34=304^@`

`["measured from north line, west is "270^@]`

`(d)`

`-2i-j" is in the third quadrant"`

`rArrtheta=tan^-1(1/2)~~27^@larrcolor(blue)"related acute angle"`

`"this angle is positioned below the x-axis in the third quad."`

`rArr"angle from north line "=180+(90-27)=243^@`

`rArr"bearing "=243^@`

Answer 2

See below

Explanation:

Using the unit vectors i and j:

From the diagram we can see that the unit vector i is the direction due east, and the unit vector j is the direction due north.

The magnitude of `ahati+bhatj` is given by:

`|| ahati+bhatj||=sqrt((a)^2+(b)^2)`

The angle the vector makes with the x axis is given by:

`alpha=arctan(b/a)`

On the diagram we will solve question a.

Magnitude:

`||2hati+3hatj||=sqrt((2)^2+(3)^2)=sqrt(13)~~3.61`

`tan(alpha)=3/2`

`alpha=arctan(3/2)=56.31^@` ( 2 .d.p.)

Bearings are always given in relation to North, this is why we need to find `beta`.

`beta=90^@-alpha`

`beta=90^@-56.31=33.7=034^@`

I will do question b, because it is in a different quadrant. This will show you how to deal with negative angles.

Magnitude:

`||4hati-hatj||=sqrt((4)^2+(-1)^2)=sqrt(17)~~4.12`

`tan(alpha)=-1/4`

`alpha=arctan(-1/4)=-14.04^@`

`beta= 90^@+|alpha|`

`beta= 90^@+|-14.04|=104^@`

You should now be able to find the other results. It pays to do a rough sketch so you know where to calculate the angles.